基本介紹
考慮一個由公理構成的證明系統P,可以將P轉換為Q。這種轉換可能有多種目的,例如:
(1)P的公理不完全被另一個系統Q接受,需要建立P和Q公理的對應關係;
(2)P公理的域與Q的域並不相同(例如,自然數與超窮數的差別),需要轉換後才有效;
(3)P公理經過轉換後更有利於證明,等等。
這樣,這種轉換也稱為 解釋,它既包含P公理的轉換,即P公理解釋為Q公理,也可以對P公理的定義域進行解釋,以驗證P公理的有效性 。
 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明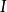 解釋性證明
解釋性證明定義1令P是命題集合,或其定義域,或參數測試樣例的集合, 是它的映射(另外的命題集合及其定義域或參數測試樣例), 是P的推論,如果存在 與 同構,則稱P具有 -解釋性證明,即
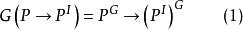 解釋性證明
解釋性證明是 解釋性證明,其中,G是同構算符。
式(1)如圖1所示。
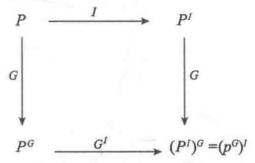 圖1
圖1可見解釋性證明是同構性證明(參見“同構證明方法”)的一種特例,它多伴有輸入自變元的調整變化作為附加條件。一個解釋性證明的實例是哥德爾對PA證明的功能解釋。另外的一種實例是歸結方法,它是通過自變元的反例輸入證明原命題的否定的不可證證明原命題。
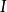 解釋性證明
解釋性證明 解釋性證明
解釋性證明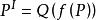 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明當式(1)中的P不是命題,而是自變元,這時 解釋P為 ,從而 ,其中Q是命題,這樣可以通過計算性的方法得到 ,並使 成為獨立的“模組”被其他證明所調用,也可以採用不同的算法得到不同的解釋。這種方法即構成“證明挖掘”(Proof Mining),或者“開放式證明”(Unwinding Proof)。這兩種稱呼,前者起源於G Kreisel,後者起源於D.Scott。
相關概念
同態與同構
 解釋性證明
解釋性證明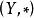 解釋性證明
解釋性證明 解釋性證明
解釋性證明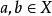 解釋性證明
解釋性證明設 和 是兩個同類型的代數系統(代數系統是集合及其運算構成的系統), 是一個映射,如果對於任意元 恆有
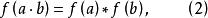 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明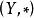 解釋性證明
解釋性證明 解釋性證明
解釋性證明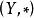 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明 解釋性證明
解釋性證明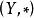 解釋性證明
解釋性證明 解釋性證明
解釋性證明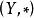 解釋性證明
解釋性證明 解釋性證明
解釋性證明則稱 是 到 的一個 同態映射,並稱 和 同態,用 表示;如果 是一個雙射,則稱 是 到 的一個 同構映射, 與 同構,用 表示。
同態和同構是布爾巴基學派提出的重要概念,它是對於結構之間關係的描述。雖然同構概念提出較晚,但其意義是極其深遠的。同構不僅是數學的證明方法,也是基本的心理結構和人類思維的基本方式 。
同構性證明
在證明中對如式(3)、式(4)、式(5)任意一命題的運用是 同構證明方法:
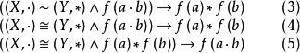 解釋性證明
解釋性證明