概念
回彈係數經常用於經驗公式中來估算內壓卸載後的凹陷深度，在沒有估算外載荷卸載後凹陷深度公式的情況下。以長輸管線上常見的 X52、X60、X70 鋼製管道為工程背景，運用 ABAQUS 軟體進行管道結構力學的非線性分析，模擬管道凹陷的形成及回彈過程。通過對比試驗與數值模擬數據，驗證有限元仿真方法的可靠性。分別在外載卸載及內壓卸載的情況下分析了各參數(載入深度、壓頭尺寸、管道尺寸、操作壓力、管材性能)對凹陷回彈係數的影響。運用 Matlab 軟體對計算結果進行非線性回歸分析，可得到回彈係數與各參數的關係表達式。
基於有限元的長輸管道凹陷回彈係數研究
凹陷是由於管壁永久塑性變形而使管道橫截面發生的總的變形，是管道的一種常見缺陷形式。管道凹陷嚴重威脅著管道的安全運行，降低管道的承壓能力，有些凹陷會立即導致管道失效。凹陷準則大多是基本無內壓時測得的凹陷特徵數據，而管道檢測通常是在受內壓的情況進行。長輸管道為高強度鋼材料，其屈服強度高，故回彈現象更加明顯。因此，了解凹陷的回彈過程並確定外載荷卸去後和內壓波動下凹陷的回彈係數對凹陷評價具有一定的意義。
相當多的國外學者對管道凹陷回彈係數進行了研究。歐洲輸氣管道事故數據組織將單純凹陷管道在內壓卸載後的回彈係數定義為1.43。研究表明，這個經驗回彈係數與實際情況存在較大的出入，偏於保守。美國 Battle 研究院考慮了內壓對凹陷深度的影響，提出回彈係數的計算方法，然而與試驗結果存在較大的出入。美國石油協會 API 579 標準給出了不同工況下的回彈係數，當操作壓力大於等於70%最大許可壓力時， 回彈係數為 1.43，否則回彈係數為1。Bastard AL考慮凹陷尺寸、管道尺寸、內壓及管材性能，提出了回彈係數公式，但該公式較為複雜，採用的管道尺寸較小，對常用的管道凹陷適用性不足。國內對凹陷回彈方面的研究較少，對不同鋼質、類型及深度等的凹陷回彈情況缺少進一步認識。
有限元模型的建立
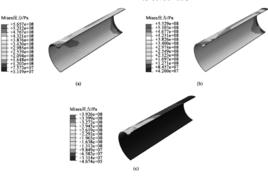
圖1 管道有限元模型示意圖選擇 ABAQUS 軟體進行有限元模型的建立及仿真。有限元模型由剛性球形壓頭和管道組成，建立管道的1/4模型進行分析。為了將凹陷區域和管道端部的相互作用降到最低，取管道長度為管道直徑的3倍，模型如圖1所示。對凹陷區域處進行格線細化，對遠離凹陷區域採用疏鬆格線，管道格線單元為 C3D8R(八節點六面體單元)。
內壓載荷施加於管道的內表面，採用準靜態的方法，將位移外載荷通過剛性壓頭施加在管道外表面。凹陷的形成及回彈的數值模擬步驟如下: (1)施加內壓，在管道的內表面施加壓力載荷；(2)壓頭載入，先使壓頭向下移動一個非常小的位移，使接觸分析平穩地建立起來，然後使壓頭向下移動位移d，使管道形成一個初始凹陷；(3)壓頭卸載，使壓頭向上移動一個較大的位移，同時解除球面壓頭和管道之間的接觸關係；(4)卸載內壓。
回彈係數影響因素分析
（1）外載作用下的回彈影響因素分析
凹陷的回彈受管道尺寸、載入深度、壓頭形狀、操作壓力及管材性能等因素的影響。首先對不同管材的回彈係數進行分析。結果表明: 管材分別為X52、X60、X70 的凹陷管道的回彈係數逐漸減小，但差別不大，如當壁厚為 10. 3 mm 時，X52與X70的回彈係數分別為0.679和0.669，平均誤差為1.49%。
①載入深度對凹陷的回彈係數影響較大；凹陷的回彈係數隨著載入深度的增大呈非線性增大；
②隨著壓頭半徑的增大，回彈係數不斷減小，即在相同的施加深度下，壓頭半徑越大，回彈量也越大，但增大的幅度有減小的趨勢；
③隨著管道壁厚的增大，回彈係數增大，即管道的徑厚比越大，凹陷在壓頭卸載後的回彈係數越小；
④操作內壓對管道的回彈係數影響較大，在載入相同深度時，內壓越大，回彈量越小。
（2）內壓作用下的回彈影響因素分析
①凹陷深度對回彈係數的影響較大，凹陷的回彈係數隨著凹陷深度的增加而減小；
②回彈係數隨壓頭半徑增大而增大，但其對內壓卸載後的回彈係數影響較小，如壓頭半徑為150 mm的凹陷回彈係數比壓頭半徑為50 mm的回彈係數大0.018，凹陷深度僅相差0. 55 mm；
③當管徑不變時，凹陷回彈係數隨著管道徑厚比的增大而增大；
④凹陷回彈係數隨著內壓的增大而增大。
研究結論
(1) 通過 Zeinoddini M 等的試驗驗證了利用有限元仿真模擬能夠合理地反映管道凹陷的形成及回彈過程，故利用有限元模擬的計算結果來對凹陷管道回彈係數進行研究是有效的。
(2) 外載卸去後，凹陷回彈係數變化範圍在0.3～0.8之間。在相同條件下，凹陷回彈係數隨壓頭載入深度增大而增大；隨著壓頭半徑、徑厚比、工作內壓的增大而減小。內壓卸去後，凹陷回彈係數變化範圍在1.05～1.3之間。在相同條件下，凹陷的回彈係數隨著凹陷深度的增加而減小；隨著壓頭半徑、徑厚比、工作內壓的增大，回彈係數增大；所研究的管材由於彈性模量相差不大，故對凹陷回彈係數幾乎沒有影響。
(3) 基於數值模擬結果，採用非線性回歸分析擬合得到單純凹陷管道的回彈係數計算公式，為外載荷卸載後和內壓卸載後的凹陷深度計算提供了一定的參考依據。
基於小波變換的落石衝擊回彈係數試驗
研究背景
落石是中國山區和丘陵地區常見的一種地質災害，很多學者都對落石災害進行了研究。Woltjer M 等指出通過模擬再現崩塌事件時必須考慮森林次冠層和落石間的相互作用問題，Dorren LKA 等提出了用於估算下墊面森林減少的落石衝擊能量的計算公式，通過考慮斜坡表面障礙物的最大高度和落石半徑建立了土體切向動力恢復係數的估算公式，Zambrano OM等建立了大塊落石運動速度的計算公式，Crosta GB等發現斜坡表面落石運動軌跡的側向擴散敏感性決定於地形的宏微特性，Vilajosana I等通過現場試驗對落石的衝擊信號進行了研究，Pichler B等通過室外試驗，通過落石衝擊坑的深度、落石的幾何尺寸和落石高度來計算落石衝擊力和衝擊時間的計算公式。Kawahara S 等分析了墊層的密度和厚度對落石衝擊力的影響，黃潤秋等通過實驗探討了平台對滾石停積作用，何思明視墊層材料為彈塑性，推導了滾石衝擊壓力計算公式。 Dorren LKA 等用GIS 技術對落石的致災區範圍進行了研究。黃潤秋等通過現場敏感性滾石試驗，發現滾石運動速度與滾石形狀、滾石質量和滾石啟動方式、斜坡植被特徵、坡面長度等因子相關，楊其新等通過室內實驗提出了落石衝擊力計算經驗公式。唐紅梅等將危岩的運動路徑分為 4個階段，運用恢復係數參考值來估算落石運動路徑，何思明等通過試驗研究了滾石坡面衝擊回彈規律。
落石碰撞回彈係數是正確估算落石運動軌跡的重要參數，由於落石問題的複雜性，採用理論方法研究落石的恢復係數的難度非常大，特別是碎石土墊層影響因子更複雜，文中基於室內落石模型試驗，考慮碎石土墊層的 4 種土石比下的 12 種乾密度，不同的落石高度獲得的衝擊力波，通過小波消噪處理，獲取最大衝擊力試驗值；根據 Hertz 碰撞理論，衝擊過程能量轉化，推到了落石衝擊力最大公式。通過試驗值反算各種土石比碎石土墊層的回彈係數的均值和最大值。
落石回彈係數
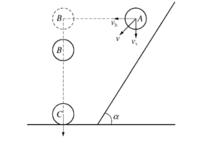圖2 碰撞分析的力學模型由Hertz碰撞理論是基於正碰撞建立的，而危岩失穩衝擊大部分都是斜碰撞，按圖2模式進行簡化，忽略切向衝擊的影響，切向速度僅提供水平位移，使危岩體由A運動到B，則B到C可等效為正碰撞過程。基於衝擊過程中能量轉化的分析，用回彈係數考慮衝擊過程中的能量損失，剩下的能量就可認為是動能與完全彈性應變能之間的轉化。如將受衝擊體視作線彈性體，可把落石衝擊視為兩物體體間的正碰撞。落石密實度由疏鬆變為密實時，回彈係數逐漸加大，土石比為4∶6時，回彈係數無論是平均值或最大值，均高於其它3 種土石比，當為密實狀態時回彈係數最大值可取達0.314，土石比為3∶7的回彈係數最小，疏鬆狀態下的均值為0.258，最大值為0.266。此結論與文獻的值趨於一致，更加細化了碎石土墊層多種狀態下的回彈係數。為偏於安全考慮，建議在落石運動路徑計算時取大值。
研究結論
（1）選取影響落石碎石土墊層的回彈係數的主因素：落石高度、落石質量、墊層土石比、含水率、密實度狀態、落石入射角。進行室內模型落石衝擊力試驗，獲得4種土石比下的12種乾密度在5種高度下的落實衝擊頻譜，通過小波消噪處理，獲得了各種情況下的最大衝擊力。
（2）基於Hertz碰撞理論，通過衝擊過程能量轉化的分析，用回彈係數考慮衝擊過程中的能量損失，剩下的能量是動能與完全彈性應變能之間的轉化，獲得了落石最大衝擊力計算式。
（3）通過試驗獲得的最大衝擊力試驗值、變形模量和泊松比，代入最大衝擊力公式，反算獲得了碎石土墊層4種土石比下的12種乾密度的回彈係數的最大值和均值圖。研究發現，碎石土回彈係數，土石比為4∶6時回彈係數無論是平均值或最大值，均高於其它3種土石比，當為密實狀態時回彈係數最大值可取達0.314，土石比為3∶7的回彈係數最小，疏鬆狀態下的均值為0.258，最大值為0.266為偏於安全考慮，建議在落石運動路徑計算式取大值。
（4）在後續研究中，依據碰撞理論建立的最大衝擊力公式，應把墊層視為彈塑性介質進一步深入細化研究。
