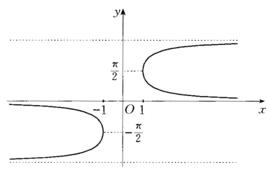
函式定義
反餘割函式（inverse cosecant function），反三角函式之一。指餘割函式 y=csc x 在區間[-π/2,0)∪(0,π/2]上的反函式。記為 y=arccsc x 或 y=csc x。它表示[-π/2,0)∪(0,π/2]上餘割值等於 x 的那個唯一確定的角，即csc(arccsc x)=x，反餘割函式的定義域是(-∞,-1]∪[1,+∞)，值域是[-π/2,0)∪(0,π/2]。
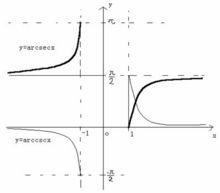圖中顏色較淡的為反餘割函式由於餘割函式在區間[-π/2,0)∪(0,π/2]上是單調連續的，因此，反餘割函式是存在且唯一確定的。引進多值函式概念後，就可以在餘割函式的整個定義域(x∈R，且x≠kπ，k∈Z)上來考慮它的反函式，這時的反餘割函式是多值的，記為 y=Arccsc x，定義域是(-∞,-1]∪[1,+∞)，值域是y∈R，且y≠kπ，k∈Z。
於是，把 y=arccsc x (x∈(-∞,-1]∪[1,+∞)，y∈[-π/2,0)∪(0,π/2])稱為反餘割函式的主值，而把 y=Arccsc x=kπ+(-1) arccsc x (x∈(-∞,-1]∪[1,+∞)，y∈R，y≠kπ，k∈Z) 稱為反餘割函式的通值。反餘割函式在區間(-∞,-1]∪[1,+∞)的圖像可由區間[-π/2,0)∪(0,π/2]上的餘割曲線作關於直線y=x的對稱變換而得到，如圖所示。
函式性質
1、定義域：{x|x≤-1或 x≥1}
2、值域：{y|-π/2≤y<0 或 0<y≤π/2 }
3、奇偶性：奇函式。（圖像漸近線為：y=0 ）
4、單調性：單調遞減區間：(-∞，-1]、[1，+∞) 【注意：絕對不能並起來】
5、最值：當x=-1時，有最小值-π/2；當x=1時，有最大值π/2
有關計算公式
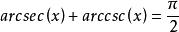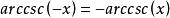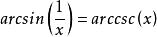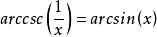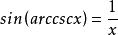反餘割函式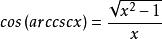
反餘割函式
反餘割函式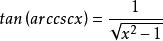
反餘割函式
反餘割函式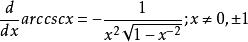
反餘割函式
反餘割函式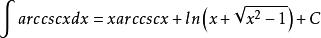
反餘割函式
反餘割函式基本原則
反三角函式主值區間選取的四項基本原則
(1)反三角函式的定義域必須最大；
(2)反三角函式值的絕對值必須最小（絕對值相等時，取正不取負）即圖形緊靠 x軸（與 x 軸等距離時，取上方不取下方）；
(3)必須包含全部正銳角（便於查表）；
(4)反三角函式的圖形必須嚴格單調，並且能連結的不間斷。
