基本介紹
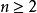 反序數
反序數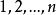 反序數
反序數排列 把n個不同的元素按一定的順序排成一行( ),稱為這n個元素的一個排列,為了方便起見,這裡只用到前n個自然數 的 排列。
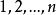 反序數
反序數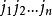 反序數
反序數n階排列由 組成的有序數組稱為一個 n階排列,通常用 表示n階排列。如2341是一個四階排列,25134是一個五階排列。
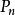 反序數
反序數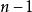 反序數
反序數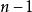 反序數
反序數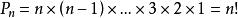 反序數
反序數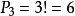 反序數
反序數 反序數
反序數自然排列 n個不同元素的所有排列的種數,通常用 表示,從n 個元素中任取一個放在第一個位置上,有n種取法;又從剩下的 個元素中任取一個放在第二個位置上,有 種取法;這樣繼續下去,直到最後只剩下一個元素放在第n個位置上,只有一種取法,於是 。如1,2,3這三個自然數組成的所有三階排列:123,132,213,231,312,321,其種數 。 是一個n階排列,它具有自然順序,稱為 自然排列(或 標準排列),在這個排列中的任何兩個數,小的數總排在大的數前面。
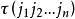 反序數
反序數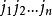 反序數
反序數反序、反序數一個排列中,如果一個大的數排在小的數之前,就稱這兩個數構成個 反序、一個排列的反序總數稱為這個排列的 反序數。用 表示排列 的反序數。
奇排列、偶排列 反序數為奇數的排列叫做 奇排列,反序數為偶數的排列叫做 偶排列。
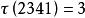 反序數
反序數例1 在四階排列2341中,共有反序21,31,41,即 ,所以2341是奇排列。
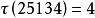 反序數
反序數在五階排列25134中,共有反序21,51,53,54,即 ,所以25134是偶排列。
 反序數
反序數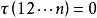 反序數
反序數 反序數
反序數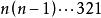 反序數
反序數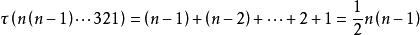 反序數
反序數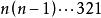 反序數
反序數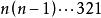 反序數
反序數例2 自然排列的反序數,所以是偶排列;而n階排列的反序數,所以,當n=4k或4k+1時,是偶排列,而當n=4k+2或4k+3時,是奇排列。
求反序時,可以從前到後將相鄰的兩個數進行比較,求出反序及反序數,也可從首位數開始找出每個數與其前面數的反序,(此時首位數的反序為0),這些反序相加即為反序數 。
相關概念與性質
在一個排列中,交換其中某兩個數的位置,而其餘各數的位置不動,就得到另一個同階的新排列。對排列施行的這樣一個交換稱為一個 對換,將相鄰兩個數對換,叫做 相鄰對換。
定理1對換改變排列的奇偶性。即經過一次對換,奇排列變成偶排列,偶排列變成奇排列。
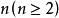 反序數
反序數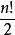 反序數
反序數推論在全部 階排列中,奇、偶排列各占一半,即各有 個。
定理2任意一個n階排列可經過一系列對換變成標準排列,並且所作對換次數的奇偶性與這個排列的奇偶性相同 。

