定義
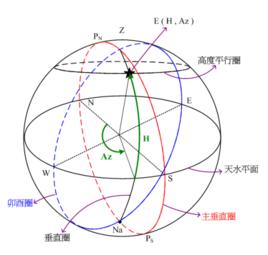
過橢球面上一點的法線，可作無限個法截面，其中一個與該點子午面相垂直的法截面同橢球面相截形成的閉合的圈稱為卯酉圈。在下圖中，PEE′即為過點P的卯酉圈 。
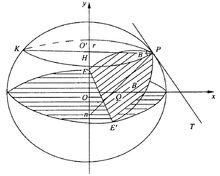圖1卯酉圈示意圖卯酉圈是一個非常拗口的名稱，該名稱的由來可參考下圖所示的羅盤簡化圖。卯酉其實就是東西向的意思。卯酉圈就是經過法線、東西走向的平面與橢球面的交線形成的閉合圈。
圖2 羅盤簡化圖計算
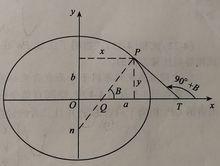圖3 子午橢圓卯酉圈的曲率半徑用N表示。
為了推求N的計算公式，如圖1所示，過P點作以O'為中心的平行圈PHK的切線PT，該切線位於垂直於子午面的平行圈平面內。因卯酉圈也垂直於子午面，故PT也是卯酉圈在P點處的切線，即PT垂直於Pn。所以PT是平行圈PHK及卯酉圈PEE'在P點處的公切線。
由麥尼爾定理知，假設通過曲面上一點引兩條截弧，一為法截弧，一為斜截弧，且在該點上這兩條截弧具有公共切線，這時斜截弧在該點處的曲率半徑等於法截弧的曲率半徑乘以兩截弧平面夾角的餘弦。
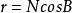卯酉圈由圖1可知，平行圈平面與卯酉圈平面之間的夾角，即為大地緯度B，如果平行圈的半徑用r表示，則有
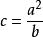卯酉圈為了簡化書寫，常引入以下符號： ，t=tanB，η=ecosB
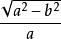卯酉圈式中，B是大地緯度，c是極點處的子午線曲率半徑，e為橢圓第一偏心率 。
此外，還有兩個常用的輔助函式：
卯酉圈
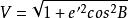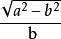卯酉圈
卯酉圈式中，e'為橢圓第二偏心率 。
又由圖3可知，平行圈半徑r就等於P點的橫坐標x，亦即
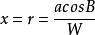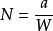卯酉圈
卯酉圈因此，卯酉圈曲率半徑
顧及以上有關公式，上式又可寫為
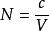卯酉圈