主要內容
如果兩個平面圖形夾在同一對平行線之間,並且為任何平行於這兩條平行線的直線所截時截得的線段都相等,那么這兩個圖形的面積相等;如果每條直線(平行於上述兩條平行線的)為兩個圖形所截得的線段的長度都有相同的比,則兩個圖形的面積也成相同的比.
相關解釋
類似地,在空間,如果兩個立體圖形夾在兩個平行平面之間,並且為任何平行於這兩個平行平面的平面所截時截得的平面片的面積都相等,那么這兩個立體圖形的體積相等;如果截兩個立體所得的兩組截面中,每個給定平面所截得的兩個不同組的截面的面積都有相同的比例,則這兩個立體的體積也成相同的比.
從現代分析學的觀點看,這個原理所斷定的實際上是:如果被積函式相等,而且積分限也相等,那么這兩個積分相等;被積函式中的常數作為一個因子可以提到積分號外面而不改變積分的值.
這一原理在西方是由卡瓦列里提出的,此後在數學中得到相當廣泛的套用.西方便稱之為卡瓦列里原理.在中國古代,三國時的劉徽和南北朝時的祖沖之父子曾考慮過相同的原理,公元5—6世紀的祖暅明確指出:“緣冪勢既同,則積不容異.”其中冪指面積,勢指關係,積指體積.這句話的意思是“若兩立體的截面面積之間的關係處處相等,則兩立體的體積之間也必有同樣的關係”.顯然,這一原理包含卡瓦列里原理的基本內容,我們稱之為“祖暅原理”或“劉祖原理”.
卡瓦列里採用多種方法來證明這一原理,這些證明都收入他的《幾何學》第7卷.其中的一個證明如下:
設夾在兩平行線PQ,RS之間的兩個任意平面圖形ABC和XYZ如圖1所示,DN和OU是平行於PQ,RS的直線,且它們在兩圖形上的截線相等.即在DN上,JK=LM,在OU上,EF+GH=TV;進而在任何與PQ等距的直線上,在ABC和XYZ中截得的線段都相等.下面證明ABC和XYZ的面積相等.
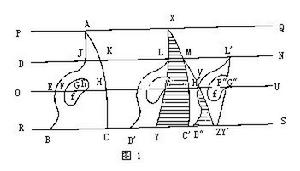
現考察平移後兩圖形不完全重合的情況.由於平移保持一直線在兩圖形上的截線的共線關係,並且它們在平移前是相等的,平移後,它們仍然相等,例如E′F′+TH′=TV.因而,如果E′F′+TH′不完全與TV重合,則它們的一部分重合,如TH′與TH′重合,於是E′F′=H′V,E′F′是平移後ABC的未蓋住XYZ的部分,H′V是平移後未被ABC覆蓋的XYZ的部分.同理可證,對每條平行於PQ的直線在兩個圖形上的截線,其未重合的部分(如果有的話)都是相等的.即這一平移有如下性質:若平移的圖形有一部分未覆蓋在另一圖形上,那么後者也一定有一部分未彼覆蓋;而且,在平移之後,兩圖形的未重合部分仍滿足原理的條件.
現在作第二次平移:平移ABC未重合的部分,使得KL,CY落在LN,YS上,則又有VB″Z重合.如前證可知,二次平移後一個圖形的仍未重合部分一定對應著另一圖形的仍然未重合的部分;它們仍滿足原理的條件,可以再順RS,DN平移,又有新的重合部分和未重合部分,這一過程可以一直進行下去,一直進行到ABC與XYZ完全重合.否則,如某一圖形有一部分未與另一圖形重合,則另一圖形也必有未重合的部分剩下.如果ABC與XYZ重合,則它們的面積相等.對立體的情況可仿此證明.說明
這一證明是巧妙而直觀的.但也有一些弱點:沒有證明按所採用的操作方法,兩個圖形未重合的部分一定是可窮竭的;也沒有證明每次平移後圖形的未重合部分一定小於原來的圖形.而且,卡瓦列里在答覆P.古爾丁(Guldin)的反對意見時聲稱,在一個圖形中(從而在另一個圖形中)“消除”未重合部分的工作可以用無窮步運算完成.
卡瓦列里的另一個證明是用古典的窮竭法作出的.對滿足一定條件的圖形(如兩圖形都是“廣義的平行四邊形”或能分解為這種四邊形的圖形)來說,這一證明是嚴格的.
