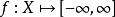 半連續
半連續 半連續
半連續 半連續
半連續 半連續
半連續如果某個函式 的上圖是閉集,我們稱 為閉函式。閉性與經典的下半連續性的概念有關,函式 是在向量 處下半連續的,如果
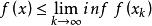 半連續
半連續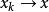 半連續
半連續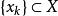 半連續
半連續 半連續
半連續 半連續
半連續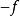 半連續
半連續對於每個滿足 的點列 成立,我們稱 是 下半連續的 (lower semicontinuous),如果它在定義域X的每一點x處都是下半連續的,我們稱 是 上半連續的(upper semicountinous),如果 是下半連續的,這些定義與針對實函式的相應定義是一致的。
相關性質定理
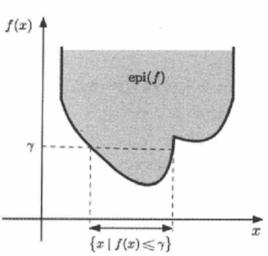
以下命題將函式的閉性、下半連續性和函式水平集的閉性聯繫起來。見圖1
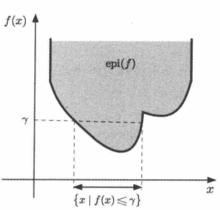 圖1
圖1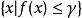 半連續
半連續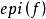 半連續
半連續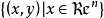 半連續
半連續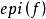 半連續
半連續圖1 函式上圖和它的水平集關係的示意圖,易見水平集 經過平移後等同於 和“切片” 的交集,這表明 為閉若且唯若所有的水平集為閉。
命題1
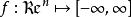 半連續
半連續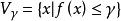 半連續
半連續 半連續
半連續 半連續
半連續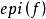 半連續
半連續對於函式
,以下各款等價:(i)水平集對每個標量均為閉;
(ii)函式為下半連續的;
(iii)集合為閉。
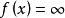 半連續
半連續 半連續
半連續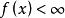 半連續
半連續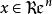 半連續
半連續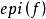 半連續
半連續 半連續
半連續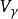 半連續
半連續 半連續
半連續證明: 如果 對所有 成立,那么結果是平凡的,顯然成立。我們假定 對至少一個 成立,這樣 就是非空的,且至少有一個非空的水平集,先來證明(i)蘊含(ii)。假定水平集 對於每個標量 都是閉的,反設
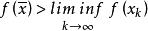 半連續
半連續 半連續
半連續 半連續
半連續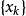 半連續
半連續 半連續
半連續對某個 和收斂到 的點列 成立,並且令 為滿足
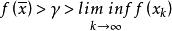 半連續
半連續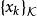 半連續
半連續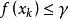 半連續
半連續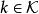 半連續
半連續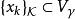 半連續
半連續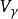 半連續
半連續 半連續
半連續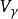 半連續
半連續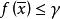 半連續
半連續 半連續
半連續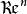 半連續
半連續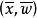 半連續
半連續下面證明(ii)蘊含(iii),假定在上為下半連續,並令為點列
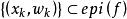 半連續
半連續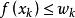 半連續
半連續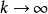 半連續
半連續 半連續
半連續 半連續
半連續的極限,於是我們有 ,進而令 ,由 在 處的下半連續性,我們得到
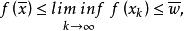 半連續
半連續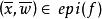 半連續
半連續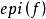 半連續
半連續於是, 故 為閉。
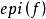 半連續
半連續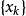 半連續
半連續 半連續
半連續 半連續
半連續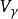 半連續
半連續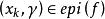 半連續
半連續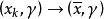 半連續
半連續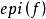 半連續
半連續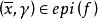 半連續
半連續 半連續
半連續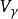 半連續
半連續最後證明(iii)蘊含(i)。假定
為閉,且令為點列,它收斂到某個且屬於對應於某個標量的水平集,於是對於所有的k成立,並且,因而由於為閉,我們有,故屬於,這意味著這個集合是閉的。
在大部分推導中,我們傾向於採用閉性的概念,而較少用到下半連續性,其中的一個原因是,不同於閉性,下半連續性是一個與定義域有關的性質。例如,由
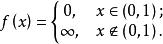 半連續
半連續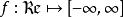 半連續
半連續定義的函式 既不是閉的也不是下半連續的;但如果把它的定義域限制到(0,1)上,就變成為下半連續。
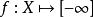 半連續
半連續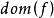 半連續
半連續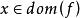 半連續
半連續 半連續
半連續另一方面,如果函式 具有閉的有效定義域且在每個 處均為下半連續,那么 必然是閉的,我們把這個結論敘述為一個命題,其證明可以據命題1證明(ii)蘊含(iii)的過程給出。
命題2
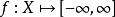 半連續
半連續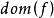 半連續
半連續 半連續
半連續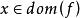 半連續
半連續 半連續
半連續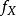 半連續
半連續令
為一函式,如果它的有效定義域是閉的,且在每個處均是下半連續的,那么函式是閉的。舉例來說,集合X的示性函式為閉若且唯若X是閉的(“當”的部分可以根據上述命題得出,而“僅當”的部分可以用上圖的定義導出),更一般地,如果是形如
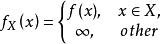 半連續
半連續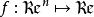 半連續
半連續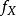 半連續
半連續的函式,其中 為連續函式,那么可以證明 是閉的若且唯若X是閉的。
最後需要指出非真的閉凸函式非常特殊:它不能在任何點上取有限值,因此它具有如下形式
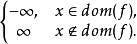 半連續
半連續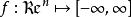 半連續
半連續 半連續
半連續 半連續
半連續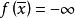 半連續
半連續 半連續
半連續 半連續
半連續 半連續
半連續為明白其中的原因,讓我們來考慮非真的閉凸函式 ,並假定存在著某個x使得 為有限.令 滿足 。(這樣的點必然存在,因為 是非真的並且 不恆等於∞),因為 是凸的,可知每個點
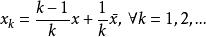 半連續
半連續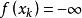 半連續
半連續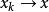 半連續
半連續 半連續
半連續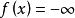 半連續
半連續都滿足 ,同時有 ,因為 是閉的,這意味著 ,從而導出矛盾,總之, 非真的閉凸函式在任何點都不能取有限值。
性質1
若干個半連續函式,它們的和是一個無處半連續的函式。
性質2
兩個半連續函式,其最小值函式並不半連續。
性質3
一個收斂的上半連續函式序列,其極限函式並不上半連續。