定義
 半素理想
半素理想 半素理想
半素理想 半素理想
半素理想 半素理想
半素理想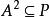 半素理想
半素理想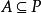 半素理想
半素理想 半素理想
半素理想 半素理想
半素理想設是半環的理想,若對於的任意理想,由必推得,則稱為的 半素理想 。
相關概念及定理
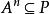 半素理想
半素理想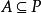 半素理想
半素理想命題1設P是半環S的理想,則P是半素理想的充分必要條件是對任意理想A,由必推得,其中n為某個自然數 。
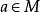 半素理想
半素理想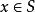 半素理想
半素理想 半素理想
半素理想定義2設M是半環S的一個子集,若對任意,存在使得,稱M為S的一個n-系統。
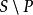 半素理想
半素理想命題3設P是半環S的理想,則P是半素的若且唯若是S的一個n-系統。
定理4設P是半環S的理想,則下列等價:
1) P是半素理想;
 半素理想
半素理想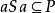 半素理想
半素理想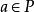 半素理想
半素理想2) 設,若,則;
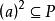 半素理想
半素理想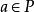 半素理想
半素理想3)必推得,其中(a)為由a生成的主理想;
 半素理想
半素理想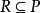 半素理想
半素理想4)必推得,其中R是S的右理想;
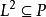 半素理想
半素理想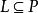 半素理想
半素理想5)必推得,其中L是S的左理想。
 半素理想
半素理想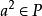 半素理想
半素理想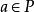 半素理想
半素理想定義5設P是半環S的理想,若對任意,由必推得,稱P為S的 完全半素理想。
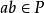 半素理想
半素理想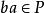 半素理想
半素理想易知,若P是半環S的完全半素理想,則由必推得。
定理6設P是半環S的素理想,則P是完全素理想的充分必要條件是P是完全半素理想。
推論7設S是交換半環,則S的素理想、完全素理想與完全半素理想三個概念是一致的。
定理8設N是半環S的理想,則
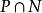 半素理想
半素理想1) 若P是S的素理想,則是N的素理想;
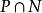 半素理想
半素理想2) 若P是S的半素理想,則是N的半素理想。
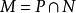 半素理想
半素理想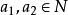 半素理想
半素理想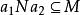 半素理想
半素理想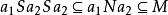 半素理想
半素理想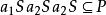 半素理想
半素理想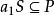 半素理想
半素理想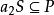 半素理想
半素理想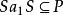 半素理想
半素理想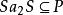 半素理想
半素理想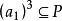 半素理想
半素理想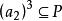 半素理想
半素理想 半素理想
半素理想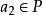 半素理想
半素理想 半素理想
半素理想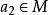 半素理想
半素理想證明:1) 記,則M是N的理想。設,若,則,於是,從而或,進而,或,得到或,推得或,這樣或,即M是N 的素理想。
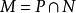 半素理想
半素理想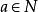 半素理想
半素理想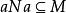 半素理想
半素理想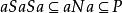 半素理想
半素理想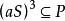 半素理想
半素理想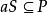 半素理想
半素理想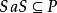 半素理想
半素理想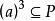 半素理想
半素理想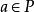 半素理想
半素理想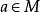 半素理想
半素理想2) 記,設,若,則,於是,,得,進而,從而,所以,即,故M是N的半素理想。
定義9若{0}是半環S的素(半素)理想,則稱S為素(半素)半環。
定理10設P是半環S的強理想,則下列等價:
1) P是素理想;
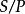 半素理想
半素理想2)是素半環;
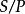 半素理想
半素理想3)中任意兩個非零理想之積非零。
定理11設P是半環S的強理想,則下列等價:
1) P是半素理想;
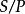 半素理想
半素理想2)是半素半環;
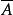 半素理想
半素理想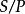 半素理想
半素理想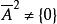 半素理想
半素理想3) 若是的非零理想,則;
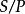 半素理想
半素理想4)不含非零冪零理想;
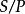 半素理想
半素理想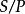 半素理想
半素理想5)不含非零冪零單側理想,即是有效半環。
 半素理想
半素理想 半素理想
半素理想 半素理想
半素理想 半素理想
半素理想 半素理想
半素理想定理10、11中的都是指S關於同餘的商半環,這兩個定理的證明只要注意到的理想(單側理想)的形式是且只是形如,其中,且,就不難了 。

