起源與發展
半監督學習的研究的歷史可以追溯到20世紀70年代,這一時期,出現了自訓練(Self-Training)、直推學習(Transductive Learning)、生成式模型(Generative Model)等學習方法。
到了20世紀90年代,對半監督學習的研究變得更加狂熱,新的理論的出現,以及自然語言的處理、文本分類和計算機視覺中的新套用的發展,促進了半監督學習的發展,出現了協同訓練(Co-Training)和轉導支持向量機(Transductive Support Vector Machine,TSVM)等新方法。Merz等人在1992年提出了SSL這個術語,並首次將SSL用於分類問題。接著Shahshahani和Landgrebe展開了對SSL的研究。協同訓練方法由Blum和Mitchell提出,基於不同的視圖訓練出兩個不同的學習機,提高了訓練樣本的置信度。Vapnik和Sterin提出了TSVM,用於估計類標籤的線性預測函式。為了求解TSVM,Joachims提出了SVM方法,Bie和Cristianini將TSVM放鬆為半定規劃問題從而進行求解。許多研究學者廣泛研究將期望最大算法(Expectation Maximum,EM)與高斯混合模型(Gaussian Mixture Model,GMM)相結合的生成式SSL方法。Blum等人提出了最小割法(Mincut),首次將圖論套用於解決SSL問題。Zhu等人提出的調和函式法(Harmonic Function)將預測函式從離散形式擴展到連續形式。由Belkin等人提出的流形正則化法(Manifold Regularization)將流形學習的思想用於SSL場景。Klein等人提出首個用於聚類的半監督距離度量學習方法,學習一種距離度量。
在半監督學習成為一個熱門領域之後,出現了許多利用無類標籤的樣例提高學習算法預測精度和加快速度的學習方法,因此出現了大量改進的半監督學習方法。Nigam等人將EM和樸素貝葉斯結合,通過引入加權係數動態調整無類標籤的樣例的影響提高了分類準確度,建立每類中具有多個混合部分的模型,使貝葉斯偏差減小。Zhou和Goldman提出了協同訓練改進算法,不需要充分冗餘的視圖,而利用兩個不同類型的分類器來完成學習。Shang等人提出一種新的半監督學習方法,能同時解決有類標籤樣本稀疏和具有附加無類標籤樣例成對約束的問題。
基本思想
半監督學習的基本設定是給定一個來自某未知分布的有標記示例集L={(x1, y1), (x2, y2), ..., (x |L|,y|L|)}以及一個未標記示例集U = {x1’, x2’, ... , x |U|’},期望學得函式f: X→Y可以準確地對示例x 預測其標記y。這裡xi, xj’ ∈X 均為d維向量,yi∈Y為示例xi的標記,|L|和|U|分別為L和U的大小,即它們所包含的示例數。
半監督學習的基本思想是利用數據分布上的模型假設建立學習器對未標籤樣例進行標籤。它的形式化描述是給定一個來自某未知分布的樣例集S=LU,其中L是已標籤樣例集L={(x1,y1),(x2,y2),,,(x|L|,y|L|)},U是一個未標籤樣例集U={xc1,xc2,,,xc|U|},希望得到函式f:XyY可以準確地對樣例x預測其標籤y。其中xi,xc1均為d維向量,ytIY為樣例xi的標籤,|L|和|U|分別為L和U的大小,即所包含的樣例數,半監督學習就是在樣例集S上尋找最優的學習器。如果S=L,那么問題就轉化為傳統的有監督學習;反之,如果S=U,那么問題是轉化為傳統的無監督學習。如何綜合利用已標籤樣例和未標籤樣例,是半監督學習需要解決的問題。
目前,在半監督學習中有三個常用的基本假設來建立預測樣例和學習目標之間的關係,有以下三個:
(1)平滑假設(Smoothness Assumption):位於稠密數據區域的兩個距離很近的樣例的類標籤相似,也就是說,當兩個樣例被稠密數據區域中的邊連線時,它們在很大的機率下有相同的類標籤;相反地,當兩個樣例被稀疏數據區域分開時,它們的類標籤趨於不同。
(2)聚類假設(Cluster Assumption):當兩個樣例位於同一聚類簇時,它們在很大的機率下有相同的類標籤。這個假設的等價定義為低密度分離假設(Low Sensity Separation Assumption),即分類決策邊界應該穿過稀疏數據區域,而避免將稠密數據區域的樣例分到決策邊界兩側。
聚類假設是指樣本數據間的距離相互比較近時,則他們擁有相同的類別。根據該假設,分類邊界就必須儘可能地通過數據較為稀疏的地方,以能夠避免把密集的樣本數據點分到分類邊界的兩側。在這一假設的前提下,學習算法就可以利用大量未標記的樣本數據來分析樣本空間中樣本數據分布情況,從而指導學習算法對分類邊界進行調整,使其儘量通過樣本數據布局比較稀疏的區域。例如,Joachims提出的轉導支持向量機算法,在訓練過程中,算法不斷修改分類超平面並交換超平面兩側某些未標記的樣本數據的標記,使得分類邊界在所有訓練數據上最大化間隔,從而能夠獲得一個通過數據相對稀疏的區域,又儘可能正確劃分所有有標記的樣本數據的分類超平面。
(3)流形假設(Manifold Assumption):將高維數據嵌入到低維流形中,當兩個樣例位於低維流形中的一個小局部鄰域內時,它們具有相似的類標籤。
流形假設的主要思想是同一個局部鄰域內的樣本數據具有相似的性質,因此其標記也應該是相似。這一假設體現了決策函式的局部平滑性。和聚類假設的主要不同是,聚類假設主要關注的是整體特性,流形假設主要考慮的是模型的局部特性。在該假設下,未標記的樣本數據就能夠讓數據空間變得更加密集,從而有利於更加標準地分析局部區域的特徵,也使得決策函式能夠比較完滿地進行數據擬合。流形假設有時候也可以直接套用於半監督學習算法中。例如,Zhu 等人利用高斯隨機場和諧波函式進行半監督學習,首先利用訓練樣本數據建立一個圖,圖中每個結點就是代表一個樣本,然後根據流形假設定義的決策函式的求得最優值,獲得未標記樣本數據的最優標記;Zhou 等人利用樣本數據間的相似性建立圖,然後讓樣本數據的標記信息不斷通過圖中的邊的鄰近樣本傳播,直到圖模型達到全局穩定狀態為止。
從本質上說,這三類假設是一致的,只是相互關注的重點不同。其中流行假設更具有普遍性。
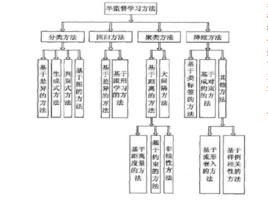
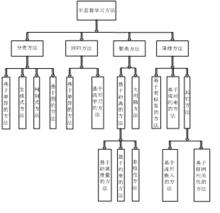
分類
 半監督學習
半監督學習SSL按照統計學習理論的角度包括直推(Transductive)SSL和歸納(Inductive)SSL兩類模式。直推SSL只處理樣本空間內給定的訓練數據,利用訓練數據中有類標籤的樣本和無類標籤的樣例進行訓練,預測訓練數據中無類標籤的樣例的類標籤;歸納SSL處理整個樣本空間中所有給定和未知的樣例,同時利用訓練數據中有類標籤的樣本和無類標籤的樣例,以及未知的測試樣例一起進行訓練,不僅預測訓練數據中無類標籤的樣例的類標籤,更主要的是預測未知的測試樣例的類標籤。從不同的學習場景看,SSL可分為四大類:
半監督分類
 半監督學習
半監督學習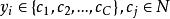 半監督學習
半監督學習半監督分類(Semi-Supervised Classification):是在無類標籤的樣例的幫助下訓練有類標籤的樣本,獲得比只用有類標籤的樣本訓練得到的分類器性能更優的分類器,彌補有類標籤的樣本不足的缺陷,其中類標籤 取有限離散值 。
半監督回歸
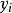 半監督學習
半監督學習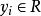 半監督學習
半監督學習半監督回歸(Semi-Supervised Regression):在無輸出的輸入的幫助下訓練有輸出的輸入,獲得比只用有輸出的輸入訓練得到的回歸器性能更好的回歸器,其中輸出 取連續值 ;
半監督聚類
半監督聚類(Semi-Supervised Clustering):在有類標籤的樣本的信息幫助下獲得比只用無類標籤的樣例得到的結果更好的簇,提高聚類方法的精度;
半監督降維
半監督降維(Semi-Supervised Dimensionality Reduction):在有類標籤的樣本的信息幫助下找到高維輸入數據的低維結構,同時保持原始高維數據和成對約束(Pair-Wise Constraints)的結構不變,即在高維空間中滿足正約束(Must-Link Constraints)的樣例在低維空間中相距很近,在高維空間中滿足負約束(Cannot-Link Constraints)的樣例在低維空間中距離很遠。
未來研究方向
經過大量研究人員的長期努力,SSL領域的研究已取得了一定發展,提出了不少SSL方法,同時已將SSL套用於許多實際領域。但目前這個領域的研究仍存在許多有待進一步解決的問題,未來的研究方向包括以下一些內容。
理論分析
目前對SSL的理論分析還不夠深入。在類標籤錯誤或成對約束不正確時學習方法的性能如何改變,選擇不同的正約束和負約束的比例會對降維的性能造成什麼影響,除了通常採用的分類精度和運算速度之外,還有沒有其他更合適的評價指標,對學習性能起到改進作用的是準確的最最佳化求解算法,還是使用的學習模型中的數據表示和學習方法,最優解對學習結果的影響有多大,未來還需要進一步探討這些問題。
抗干擾性與可靠性
當前大部分SSL利用的數據是無噪聲干擾的數據,而且依賴的基本假設沒有充分考慮噪聲干擾下無類標籤數據分布的不確定性以及複雜性,但是在實際套用中通常難以得到無噪聲數據。未來需要研究如何根據實際問題選擇合適的SSL方法,更好地利用無類標籤的樣例幫助提高學習的準確性和快速性,並減小大量無類標籤數據引起的計算複雜性,可以考慮引入魯棒統計理論解決該抗噪聲干擾問題。此外,大量實驗研究證明當模型假設正時,無類標籤的樣例能夠幫助改進學習性能;而在錯誤的模型假設上,SSL不僅不會對學習性能起到改進作用,甚至會產生錯誤,惡化學習性能。如何驗證做出的模型假設是否正確,選擇哪種SSL方法能夠更合適地幫助提高學習性能,除了己有的假設之外,還可以在無類標籤的樣例上進行哪些假設,新的假設是否會產生新的法,SSL能否有效用於大型的無類標籤的數據,這些問題還有待未來研究.此外,導致SSL性能下降的原因除了模型假設不符合實際情況外,還有學習過程中標記無類標籤的樣例累積的噪聲,是否還有其他原因使無類標籤的樣例造成學習能力的下降,也是未來需要進一步研究的問題。
訓練樣例與參數的選取
通常訓練數據是隨機選取的,即有類標籤的樣例和無類標籤的樣例獨立同分布,但是在實際套用中,無類標籤的樣例可能來自與有類標籤的樣例分布不同或未知的場景,並且有可能帶有噪聲。未來的研究需要找到一個好的方法將SSL和主動學習相結合,選取有利於學習模型的訓練樣例,並確定SSL,能夠有效進行所需要的有類標籤的樣本數量的下界。此外,許多研究人員將SL和UL二算法擴展用於SSL,但是許多這些算法是根據先驗信息得到訓練數據集的參數,並利用這些參數改進算法在SSL中的性能.目前都是人工選取一種SSL方法,並設定學習數,保證SSL的性能優於SL和UL,但是當選取的SSL方法與學習任務不匹配或者參數的設定不合適時,會成SSL的性能比SL或UL更差.如何自動根據學習任務選取合適的SSL方法並準確得到參數是未來SSL需要深入研究的內容,可以考慮用全貝葉斯學習理論解決。
最佳化求解
從各種SSL算法的實現過程可以看出,SSL問題大多為非凸、非平滑問題,或整數規劃和組合最佳化問題,存在多個局部最優解,例如求解SSL產生式方法目標函式的EM算法只能得到局部極大值目前主要採用各种放松方法把目標函式近似轉化為凸或連續最最佳化問題,不易得到全局最優解,算法的時空複雜性很高,問題的求解依賴於最最佳化理論的突破,未來需要研究新的算法求解全局最優解。
研究拓展
SSL從產生以來,主要用於實驗室中處理人工合成數據,未來的研究一方而需要討論SSL可以顯著提高哪些學習任務的性能,拓展SSL在現實領域的實際套用,另一方而需要制定出一個統一的令人信服的SSL方法的使用規程。此外,目前有許多的半監督分類方法,而對半監督回歸問題的研究比較有限。未來有待繼續研究半監督分類和半監督回歸之間的關係,並提出其他半監督回歸方法。