十進小數的發展歷史
進小數的出現,是數學史上的一件大事。美國數學史家卡豹利就曹熟為十進小數是近代數學史上關於針算基礎方面的三大發明之一,他就:“近代舒算的異常勢力是由於三大發明:印度舒數法、十進分數和對數,因此介招一下十進小數的發展歷史是有益處的。
在西洋數學史上常常把十進小數的發明歸功於歐洲人,特別歸功於斯台文(F.stevin,1548一1620)等人,這是不正確的。實際上,中國、印度和中亞都在歐洲人之前使用了十進小數。
我國是最早採用十進位值制計數的國家 .這種計數法使得我 國古代在數值計算方面長期處於領先地位 ,小數也是我 國最早發 明並運用 的 ,它經歷 了一個較長的發展歷程.十進小數是在實際度量和整數運算 (如除法、開方) 的需要中產生和發展起來的.隨著社會 的發展 ,對度量精度的要求逐漸提高 ,反 映在數學上 ,就是對數量表示的精確程度要求的提高。
引證解釋
 十進小數
十進小數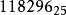 十進小數
十進小數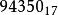 十進小數
十進小數=(94305.17)
這樣的數 ,用附在整數位後面 的小字來表明小數 。
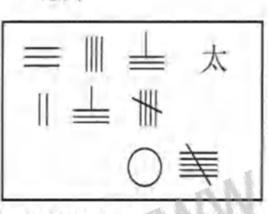
十進小數的具體使用(“九章算術”注)
方田”章圓田術注:“…七十五(平方)寸,開方除之,下至秒、忽,又一退法.求其微數、微數無名,知以為分子,以十L習為分母,釣作五分忽之二,故得股八寸六分六廈二秒五忽五分忽之二”.就是先把乃平方寸化成750000000000平方忽,開平方得整數566025忽,還有剩餘,再往下求就得小數,劉徽把這數阱“微數”.劉徽將求出的第一位“微數”數字 。a做分子,以10為分母來表示,既 “約作五分忽之二”,就是把 約作 (顯然a1應是4,).總起來看也就是
少廣”章開方術注:“……凡開積為方,……求其微數,微數無名者,以為分子,其一退以十為母,其 再退以百為母,退之彌下,其分彌袖.……”.殷N是被開平方數,其平方根的整數部分為a忽,還有剩餘為r (平方忽),既
少廣”章開立方術注:“術亦有創法命分者,不如故篡開方,以微數為分也.”這段韶的意思不如前兩段那樣明顯,但“以微數為分”這句韶可創荻明,劉徽也是用十進分數來處理小數的.
1.方田”章圓田術注:“…七十五(平方)寸,開方除之,下至秒、忽,又一退法.求其微數、微數無名,知以為分子,以十L習為分母,釣作五分忽之二,故得股八寸六分六廈二秒五忽五分忽之二”.就是先把乃平方寸化成750000000000平方忽,開平方得整數566025忽,還有剩餘,再往下求就得小數,劉徽把這數阱“微數”.劉徽將求出的第一位“微數”數字 。a做分子,以10為分母來表示,既 “約作五分忽之二”,就是把 約作 (顯然a1應是4,).總起來看也就是
2.少廣”章開方術注:“……凡開積為方,……求其微數,微數無名者,以為分子,其一退以十為母,其 再退以百為母,退之彌下,其分彌袖.……”.殷N是被開平方數,其平方根的整數部分為a忽,還有剩餘為r (平方忽),既
3.少廣”章開立方術注:“術亦有創法命分者,不如故篡開方,以微數為分也.”這段韶的意思不如前兩段那樣明顯,但“以微數為分”這句韶可創荻明,劉徽也是用十進分數來處理小數的.
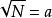 十進小數
十進小數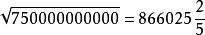 十進小數
十進小數十進小數的表示方法
開始,人類只能用整數表示數量,繼而在所表示 的數量的末尾附註 “有餘 ”、“有 奇 ”或“強”、“弱”等字樣 ,以表示該數量與實際量之間的差異 ,當需要用數來比較精確地表明這種差異的時候 ,就逐漸形成了兩種表示方法:
1.一種是用分數來表示不足整數的剩餘部分;
2.另一種是發展度量衡系統,採用更小的度量衡單位來表示有關的量。