簡介
在幾何學中,十二面體是(希臘語δώδεκαdōdeka)是具有十二個平面的多面體。 最熟悉的十二面體是有規則的正十二面體,它是柏拉圖式的十二面體。 還有三種星形十二面體,它們被構造為凸形的星體形狀。(見文末的圖冊)
五角十二面體(pyritohedron)是不規則的十二面體,具有與有規則的十二面體相同的拓撲結構,但是具有金字塔式的對稱性。 被認為是五角十二面體的極限情況的菱形十二面體具有八面體對稱性。還有大量的其他十二面體。
五角十二面體
五角十二面體是五個有規則的柏拉圖式體之一,可以由其Schläfli符號{5,3}表示。
雙面多面體是常規的二十面體{3,5},每個頂點都有五個等邊三角形。
在晶體學中,有兩個重要的十二面體可以作為立方晶系的一些對稱類型中的晶體形式發生,其在拓撲學上等同於正十二面體,但是對稱較少。
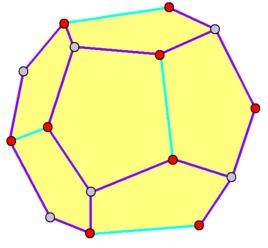
吡哆醛
吡哆醛是十二面體,具有三面體(T)對稱性。 像正常的十二面體一樣,它有十二個相同的五邊形面,三個會聚在20個頂點的每個頂點。但是,五邊形不限於規則的,底層的原子排列沒有真正的五重對稱軸。 它的30個邊緣被分成兩組 - 包含相同長度的24和6個邊。 鏇轉對稱的唯一軸是三個相互垂直的雙重軸和四個三重軸。
儘管在晶體中不存在規則的十二面體,但是在黃鐵礦的晶體中卻有五角十二面體的形式,這可能是發現規則柏拉圖式固體形式的靈感。 注意,真正的正十二面體可以作為具有二十面體對稱性的準晶體的形狀發生,其包括真正的五倍鏇轉軸。
水晶黃鐵礦
它的名字來自黃鐵礦顯示的兩種常見的晶體之一,另一種是立方體。
笛卡爾坐標
原始立方體的八個頂點的坐標為:(±1,±1,±1);
交叉邊的12個頂點的坐標為:
(0,±(1 + h),±(1-h2))
(±(1 + h),±(1 - h2),0)
(±(1 - h2),0,±(1 + h))
其中h是立方體上方的楔形“屋頂”的高度。 當h = 1時,六個交叉邊緣退化為點,形成菱形十二面體。 當h = 0時,交叉邊緣被吸收在立方體的小平面上,並且,菲律賓的圓錐體減少到立方體。 當h =(√5 - 1)/2(黃金比例的倒數)時,結果是一個規則的十二面體。
幾何自由度
吡哆醛具有幾何自由度,在合線邊緣的一個極限處具有立方凸包的極限情況,並且作為另外的極限的菱形十二面體退化為長度為零。 正常十二面體代表了所有邊緣和角度相等的特殊中間情況。
雙重三角陀螺
正規十二面體的對稱形式可以被構造為由三角形構成的多面體的雙重連線,稱為三角形陀螺儀。 它具有D對稱性,順序12;它具有2組在頂部和底部的3個相同的五邊形,連線在側面的6個五邊形,上下交替。 該形式具有六邊形橫截面,並且相同的副本可以作為部分六邊形蜂窩連線,但所有頂點將不匹配。
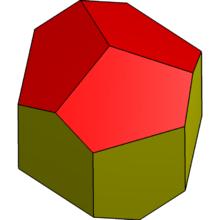 十二面體
十二面體菱形十二面體
菱形十二面體是具有十二個菱形面和八面體對稱面。 它是雙重對稱的立方八面體(阿基米德體),並且在自然界中以晶體形式出現。
菱形十二面體可以看作是一個簡併的吡哆醛,其中6個特殊邊緣已經減少到零長度,將五邊形減少成菱形面。
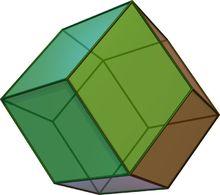 十二面體
十二面體另一個重要的菱形十二面體,比林斯基十二面體,具有與菱形三角陶腦相同的十二個面,即對角線與黃金比率之比。 它也是一個環帶多面體,並由Bilinski在1960年描述。也可以發生在非周期性的填充物以及菱形三角體,菱形二十面體和菱形六面體。
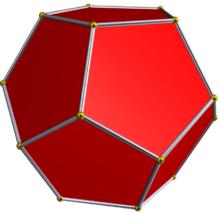 幾種十二面體
幾種十二面體