歷史背景
區域分解法最原始的思想可以追溯到1870年德國數學家H.A.Schwarz提出的用於論證非規則橢圓型方程解的存在性與唯一性的著名的Schwarz交替法。直到本世紀五十年代,才有人把Schwarz方法用於計算。八十年代以來,隨著並行計算機的問世及日益普及,經典的串列計算格局不適應於並行計算機,如何構造高度並行的算法成為了關注的焦點。區域分解算法即在這樣的背景下應運而生。
定義
區域分解方法是將計算域分解為若干子域,分別求解再進行綜合的一種數值計算方法。此種方法便於在各子域中運用適應其特點的數學模型、計算方法和格式,使總體解更符合實際,並有利於採用並行算法,加快運算速度。
分類
有關區域分解法的類型大致上可以分為重疊型區域分解法和不重疊型區域分解法兩種,下面簡單介紹這兩種方法。
不重疊型區域分解法
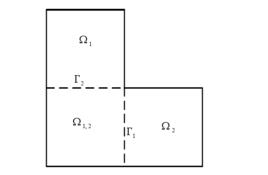
不重疊型區域分解法主要是基於有限元框架,將原求解區域S分解為若干子域的並,並且要求各子域之間互相不重疊。在採用有限元方法對所求問題進行計算時,首先要對求解區域進行區域剖分,按照剖分區域之間是否存在內交點,不重疊型區域分解法大體上可以分為兩種類型,其中沒有內交點的情形計算起來相對容易一些,而有內交點情形處理起來比較困難,必須使用專門的預處理技巧加以處理。
重疊型區域分解法
重疊型區域分解法以經典的Schwarz交替法為理論依據,將原求解區域S初始剖分為若干子域的並。這裡各子域之間互相重疊。在運用Schwarz交替法進行求解的過程中,由相鄰子區域間互相重疊的部分傳遞信息。Schwarz算法可以將所要求解原問題大型的區域分解成若干互相重疊子域,即把對原複雜問題求解的主要步驟轉化為在其各子區域內獨立進行,這樣不僅縮小了問題的計算規模,而且可以選擇更加適合所求問題的快速算法,使得計算靈活高效。在重疊型區域分解算法的基礎上可以構建許多高效的算法,因此該方法在求解實際大規模問題方面非常的重要。
意義
流動問題的數值模擬方法套用於實際工程問題,往往涉及到求解大型偏微分方程組。對應的計算區域往往是高維的,大範圍的,且其形態可能很不規則,因而給計算帶來很大的困難。另外,值得注意的是數值方法只能分辨相對於格線尺度而言的長波現象。如果為了提高解析度而減小格線的尺度,遇到的最大問題將是計算機的容量和速度的限制。超級計算機的問世雖然解決了一些實際問題,但很多領域的流動數值模擬,如大氣研究,太空飛行器的設計,數值天氣預報等的問題用現有的超級計算機仍然無法得到解決。
面對新的問題,伴隨著本世紀八十年代以來並行計算機和並行算法的發展,作為偏微分方程數值解的新技術的區域分解算法(DDM )驟然崛起。
簡而言之,區域分解算法是把區域分解為若干個子區域,子區域應儘可能規則,從而將原問題的求解轉化為在子域上的求解。
區域分解方法的優越性集中體現在以下幾個方面:
1.它把大問題化為若干個小問題,從而縮小了計算規模。這對於克服計算機容量和速度的限制具有極大的意義。
2.子區域如果形狀規則,其上或者允許使用熟知的快速算法,如快速Fourier變換(FFT)譜方法,譜方法等,或者己經有解這類規則問題的高效軟體備用。
3.允許使用局部擬一致格線而無需用整體擬一致格線,甚至各子域可以用不同離散方法進行計算。這對於形態極不規則的問題具有極大的靈活性。以鍋爐燃燒問題為例,爐體部分與煙囪部分幾何尺寸相差很大,整體計算為了對付煙囪部分而不得不把格線加得很密;另外,由於採用有限差分方法,不得不人為地加入障礙區,從而大大增加了計一算量。而如果採用區域分解算法,則可以把煙囪和爐體部分分別處理,那么上述兩個問題均可得到較好的解決。
4.允許不同子域選用不同的數學模型,以便整體模型更適合於工程物理實際情況。例如氣體繞飛行體流動的問題,在邊界層附近為枯性流動,而在邊界層外則為無粘流動,兩者的數學模型迥然不同。如果採用區域分解算法:就可以較好地實現在不同子域上選用相應的數學模型。
5.算法高度並行,即計算的主要步驟是在各子域中獨立進行的。