定義
若一個四邊形中存在相鄰兩邊的平方和等於一條對角線的平方,則稱這個四邊形為勾股四邊形,這兩條相鄰的邊稱為這個四邊形的勾股邊.
簡介
勾股四邊形是以勾股定理為原型演化出的一類四邊形。
一般分為兩種情況,一類是含有直角的四邊形,根據定義易知含有直角的四邊形一定是勾股四邊形
另一類是不含直角的四邊形,情況稍微複雜些,常常需要變換線段來證明是否為勾股四邊形
常見圖形
例如矩形、直角梯形、正方形、以直徑為對角線的圓內接四邊形
例題
1如圖(圖②)所示將△ABC繞頂點B按順時針方向旋轉60°,得到△DBE,連線AD,DC,已知∠DCB=30°。求證:DC²+BC²=AC²
即四邊形ABCD是勾股四邊形
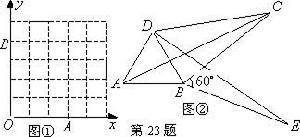
2 以△ABC的邊AB,AC邊,向三角形外作正方形ABDE和ACFG,連線CE,BG相交於點O,P是線段DE上的任意一點,求證:四邊形OBPE是勾股四邊形。
答案:根據SAS證明三角形BCA和BAG全等,那么角AEC和ABG相等,設AB和EO交於點K,那么角KOB=角KAE,及證明了三角形BOE是直角三角形了,所以原命題得證了
3已知格點(小正方形的頂點)O(0,0),A(3,0),B(0,4),請你在圖①中畫出以格點為頂點,OA、OB為勾股邊且對角線相等的勾股四邊形OAMB。
答案:(3,4)和(4,3)
