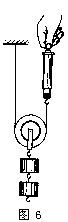
定義
使用時,軸隨物體一起移動的滑輪叫做動滑輪。動滑輪可以看做是一個省力槓桿,O為槓桿的支點,滑輪的軸是阻力的作用點。被提升的物體對軸的作用力是阻力,繩對輪的作用力是動力。提升重物時,如果兩邊繩子平行,動力臂為阻力臂的兩倍;動滑輪平衡時,動力為阻力的一半。因此若不計動滑輪自身所受的重力,使用動滑輪可以省一半力,但這時卻不能改變用力的方向,向上拉繩才能將重物提起。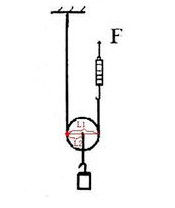 ·
·動滑輪的特點
使用動滑輪能省一半力,費距離。這是因為使用動滑輪時,鉤碼由兩段繩子吊著,每段繩子只承擔鉤碼重的一半。使用動滑輪雖然省了力,但是動力移動的距離是鉤碼升高的距離的2倍,即費距離。不能改變力的方向。隨著物體的移動而移動。另外,在生活中不能忽略動滑輪本身的質量,所以在動滑輪上升的過程中做了額外功,降低機械效率。
定義1:軸的位置隨被拉物體一起運動的滑輪稱為動滑輪。
定義2:若將重物直接掛在滑輪上,在提升重物時滑輪也一起上升,這樣的滑輪叫動滑輪。
定義3:如果人站在所拉物體上拉動繩子時,相對地面運動的滑輪反而相當於定滑輪,固定不動的為動滑輪,因此動滑輪的定義為相對於施力的人來說如果滑輪運動則為動滑輪,否則為定滑輪。
歷史由來
關於滑輪的繪品最早出現於一幅西元前八世紀的亞述浮雕。這浮雕展示的是一種非常簡單的滑輪,只能改變施力方向,主要目的是為了方便施力,並不會給出任何機械利益。在中國,滑輪裝置的繪製最早出現於漢代的畫像磚、陶井模。在《墨經》里也有記載關於滑輪的論述。古希臘人將滑輪歸類為簡單機械。早在西元前400年,古希臘人就已經知道如何使用複式滑輪了。大約在西元前330年,亞里士多德在著作《機械問題》(《MechanicalProblems》)里的第十八個問題,專門研討“複式滑輪”系統。阿基米德貢獻出很多關於簡單機械的知識,詳細地解釋滑輪的運動學理論。據說阿基米德曾經獨自使用複式滑輪拉動一艘裝滿了貨物與乘客的大海船。西元一世紀,亞歷山卓的希羅分析並且寫出關於複式滑輪的理論,證明了負載與施力的比例等於承擔負載的繩索段的數目,即“滑輪原理”。[1]
1608年,在著作《數學紀要》(《MathematicalCollection》)里,荷蘭物理學者西蒙·斯芬表明,滑輪系統的施力與負載之間移動路徑的長度比率,等於施力與負載之間的反比率。這是雛型的虛功原理。
1788年,法國物理學者約瑟夫·拉格朗日在巨著《分析力學》(《Mécaniqueanalytique》)里,使用滑輪原理推導出虛功原理,從而揭起了拉格朗日力學的序幕。
性質
一個動力臂(L1)為阻力臂(L2)二倍的省力槓桿,省1/2力多費1倍距離,不能改變力的方向,但需要一定的前提了解力作用在輪和軸上時,動滑輪的作用:可以省力,但不能改變力的方向。
定滑輪雖然可以改變力的方向,不省距離,不省力。
實驗
儀器器材演示滑輪組(J2121型),測力計2個及2個以上,鉤碼,細繩及支架。
實驗方法
1.取一細繩跨過滑輪,細繩的一端固定在支架或橫樑上,另一端系在測力計的鉤上。測力計拉動細繩,滑輪隨之移動,這樣的滑輪叫動滑輪。
2.在滑輪框架的鉤上掛鈎碼,使滑輪兩邊的兩根細繩在豎直方向上,手通過測力計拉住繩子的一端。當滑輪平衡、或將滑輪和它下面的鉤碼一起勻速提升,記下測力計的讀數。改變鉤碼重,重複以上實驗,並記下測力計的讀數。
3.實驗結果表明,在實驗誤差允許的範圍內,測力計讀數僅為鉤碼重的一半。由此可以得出結論:使用動滑輪能省一半力。
4.按圖1.47-3所示,用兩個相同的測力計吊住繩子的兩端,並使滑輪兩邊的繩子保持豎直,測力計指針不與標尺相碰。可以看到,兩個測力計的讀數相等,並且兩個讀數之和等於動滑輪和鉤碼的總重。若滑輪本身重可以忽略,則動滑輪兩邊的每根細繩所承受的力是相等的,並且承擔所掛物體重的一半。
注意事項
實驗的演示中,會出現測力計讀數偏大的情況,這是由於在提升重物的同時還要提升動滑輪,還要克服摩擦力的緣故與滑輪有關的摩擦有兩種,一種是滑輪和轉軸之間的摩擦;另一種是繩子與滑輪的摩擦。
還有一種是繩子的自重,國中物理計算題中一般忽略繩重及摩擦。
省力計算
一、F=G/2(理想化,不計滑輪的重量且只有一個動滑輪)二、F=(G+G動滑輪)/2(考慮了動滑輪的重量且只有一個動滑輪)
三、F=(G+G動滑輪)/n(n代表接在動滑輪上的繩子的段數,這是一個滑輪組)
特殊使用方法
物體掛在動滑輪一側繩子上,拉動滑輪的輪軸,如圖: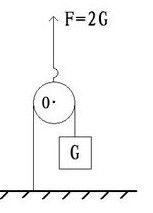 ·
·動滑輪特殊使用時,不省力,所用的力是重物重力的2倍,繩子移動距離是重物移動距離的二分之一。相當於正常動滑輪的相反效果。