定義
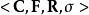 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理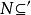 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理經典Löwenheim–Skolem 定理聲稱對於標識(signature)為 的任何可數一階邏輯語言L和L-結構 M,存在一個可數無限基本子結構 這個定理的自然和有用的推論是所有一致的L-理論都有可數的模型。
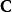 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理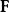 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理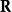 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理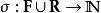 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理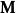 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理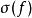 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理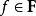 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理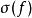 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理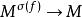 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理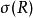 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理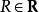 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理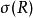 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理這裡的標識由常量集合 、函式集合 、關係符號集合 、和表示函式和關係符號的元數的函式 組成。在這個上下文中L-結構,由底層集合(經常指示為“M”)和L的函式和關係符號的釋義組成。L的常量在M中的釋義就是 的元素。類似的, -元函式 被指派為M中的 -元函式 的圖,而 -元關係 的釋義被指派為M中的 -元關係。語言L是可數的,如果在L中的常量、函式和關係符號是可數的。
例子
一個周知的不可數模型是所有實數的集合,帶有次序關係 "<" 作為唯一的關係,和加法與乘法作為函式。有序域的公理是一階句子;最小上界公理不是一階的而是二階的。這個定理蘊涵了實數域的某個可數無限的子域,因此不同於實數域,但滿足了實數域所滿足的所有一階句子。(作為可數的有序域,它不能滿足最小上界公理)。例如,特定多項式方程有解(在這個模型中)的斷言是一階句子,因此在斷言了其存在的可數子模型中是真的,若且唯若它在實數域中是真的。
數學家考慮的多數數學結構,特別是多數範疇的多數成員,是這裡定義意義上的模型。Löwenheim–Skolem 定理告訴我們如果它們是不可數的,它們不能被任何一階句子的集合唯一性的選取出來。
證明梗概
對於在模型M中為真的如下形式的一階句子
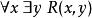 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理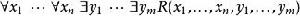 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理或
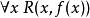 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理有一個Skolem 函式f,就是說映射x到斷言了其存在的y的函式,使得
在M中為真。因為有很多這樣的y的值,必須啟用選擇公理來推出 Skolem 函式的存在。
這個模型的某些成員可以直接用一階公式來定義,就是說,它們的存在被如下形式的句子所斷言
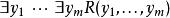 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理並且因為只有可數多個一階公式,只有可數多個成員可以用這種方式直接定義。
證明的想法是: 開始於這個模型的所有一階可定義成員的集合,並接著在所有 Skolem 函式下閉合它。這個閉包必定最多是可數無限的。這個模型的子集是這個定理斷言了其存在的子模型。
更一般的表述
上述定理假定了有限或可數無限的語言。更一般的 Löwenheim-Skolem 定理做其他有關基數的假定。類似於這個經典定理的某些定理,斷言更小的子模型的存在(“向下” Löwenheim-Skolem 定理);其他一些斷言更大基數的模型的存在(“向上” Löwenheim-Skolem 定理)。
邏輯中的定義和證明
 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理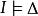 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理勒文海姆-斯科倫 定理: 如果 是一個含有 有限可數個數的命題組成的集合,並且集合 是 可以滿足的( SAT),那么至少存在一個模型(或叫作指派,或叫作解釋(Interpretation)) 用符號記作 I, ,且這個模型 I 指派解釋也是可數的
證明:
 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理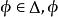 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理前提:在語言集合L中如果我們有一個可滿足式的有限可數命題公式的集合 ,且 是 中的命題公式
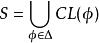 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理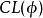 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理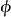 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理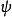 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理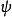 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理如果我們有一個集合,用字母記作 S ,並且 ,其中集合 是由命題公式 轉換成子句結構(Clause)所組成的集合,我們有一個定理(記作Th): 如果 是可滿足式的(Satisfaisable)公式,若且唯若Clause( )也是可滿足式的,通過這個定理,我們確保S是可滿足的,並且也是可數的
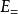 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理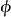 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理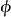 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理如果我們有一個基於語言集合L的等價公理集合,記作 (該集合是為了用於Skolemisation方法中,也就是 在轉化成Clause( )過程中,去除有限量詞 的方法Skolemisation,化為Skolem範式)
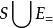 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理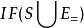 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理那么很顯然 也是可滿式的集合,那么 同樣是可滿足的
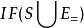 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理由於語言集合L中的元素是可數的 所以 是也是有限可數的集合
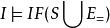 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理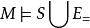 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理如果我們有一個模型,記作 I 且 ,赫爾不蘭特定理(Theoreme de Herbrand)告訴我們如果我們要構造一個模型M,並且 ,那么模型M的模型解釋指派域(記作)D是一個以I(t)為元素的指派域(其中t是在S中的所有的項),那么模型M是通過Congurence關係來解釋指派等價性關係(Egalite)
由於我們說語言理合L是可數的,那么指派解釋域D也是可數的
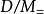 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理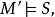 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理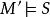 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理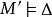 勒文海姆–斯科倫定理
勒文海姆–斯科倫定理那么我們可以構造另一個模型M',並且基於解釋域 (我們通過等價關係來指派解釋等價性)且 那么M'必然也是可數的,那么根據Th定理, ,那么我們就可以說
所以我們證明了勒文海姆-斯科倫定理。
