基本釋義
前綴表達式就是前序表達式,是一種是由波蘭數學家揚·武卡謝維奇1920年引入的數學表達式方式。
例如,- 1 + 2 3,它等價於1-(2+3)。
注意事項
後綴表達式源自於前綴表達式,為了區分前綴和後綴表示,通常將後綴表示稱為逆波蘭表示;因前綴表示並不常用,所以有時也將後綴表示稱為波蘭表示。
運算優勢
前綴表達式是一種十分有用的表達式,將中綴表達式轉換為前綴表達式後,就可以只依靠出棧、入棧兩種簡單操作完全解決中綴表達式的全部運算。
例如,(a+b)*(c+d)轉換為*,+,a,b,+,c,d。
後面的前綴表達式的運算方式為:如果當前字元(或字元串)為數字或變數,則壓入棧內;如果是運算符,則將棧頂兩個元素彈出棧外並作相應運算,再將結果壓入棧內。當前綴表達式掃描結束時,棧里的就是中綴表達式運算的最終結果。對比中綴運算的步驟,不難發現前綴運算在計算機上的優勢。
求值方法
對前綴表達式求值,要從右至左掃描表達式,首先從右邊第一個字元開始判斷,若當前字元是數字則一直到數字串的末尾再記錄下來,若為運算符,則將右邊離得最近的兩個“數字串”作相應運算,然後以此作為一個新的“數字串”並記錄下來;掃描到表達式最左端時掃描結束,最後運算的值即為表達式的值。
例如:對前綴表達式“- 1 + 2 3”求值,掃描到3時,記錄下這個數字串,掃描到2時,記錄下這個數字串,當掃描到+時,將+右移做相鄰兩數字串的運算符,記為2+3,結果為5,記錄下5這個新數字串,然後繼續向左掃描,掃描到1時,記錄下這個數字串,掃描到-時,將-右移做相鄰兩數字串的運算符,記為1-5,結果為-4,此時關於這個表達式的全部運算已完成,故表達式的值為-4。
表達對照
中綴表達式轉化為前綴表達式的例子:
a+b ---> +,a,b
a+(b-c) ---> +,a,-,b,c
a+(b-c)*d ---> +,a,*,-,b,c,d
a+1+3 ---> +,+,a,1,3
轉換算法
(1) 首先構造一個運算符棧(也可放置括弧),運算符(以括弧為分界點)在棧內遵循越往棧頂優先權不降低的原則進行排列。
(2)從右至左掃描中綴表達式,從右邊第一個字元開始判斷:
如果當前字元是數字,則分析到數字串的結尾並將數字串直接輸出。
如果是運算符,則比較優先權。如果當前運算符的優先權大於等於棧頂運算符的優先權(當棧頂是括弧時,直接入棧),則將運算符直接入棧;否則將棧頂運算符出棧並輸出,直到當前運算符的優先權大於等於棧頂運算符的優先權(當棧頂是括弧時,直接入棧),再將當前運算符入棧。
如果是括弧,則根據括弧的方向進行處理。如果是右括弧,則直接入棧;否則,遇左括弧前將所有的運算符全部出棧並輸出,遇右括弧後將左右的兩括弧一起刪除。
(3) 重複上述操作(2)直至掃描結束,將棧內剩餘運算符全部出棧並輸出,再逆綴輸出字元串。中綴表達式也就轉換為前綴表達式了。
實例分析
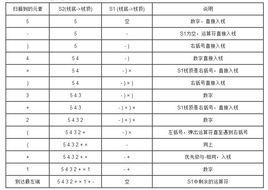
將中綴表達式“1+((2+3)*4)-5”轉換為前綴表達式。
| 中綴表達式 | 前綴表達式 | (棧頂)運算符棧(棧尾) | 說明 |
| 5 | 5 | 空 | 5,是數字串直接輸出 |
| - | 5 | - | -,棧內無運算符,直接入棧 |
| ) | 5 | -) | ),直接入棧 |
| 4 | 5 4 | -) | 4,是數字串直接輸出 |
| * | 5 4 | -)* | *,棧頂是括弧,直接入棧 |
| ) | 5 4 | - ) * ) | ),直接入棧 |
| 3 | 5 4 3 | - ) * ) | 3,是數字串直接輸出 |
| + | 5 4 3 | - ) * ) + | +,棧頂是括弧,直接入棧 |
| 2 | 5 4 3 2 | - ) * )+ | 2,是數字串直接輸出 |
| ( | 5 4 3 2+ | - ) * | (,與棧里最後一個)抵消,並釋放它們之間的+ |
| ( | 5 4 3 2+* | - | (,方法與上類同,請參考下一目錄 |
| + | 5 4 3 2+* | -+ | +,優先權大於等於棧頂運算符,直接入棧 |
| 1 | 5 4 3 2+*1 | -+ | 1,是數字串直接輸出 |
| 空 | 5 4 3 2+*1+- | 空 | 掃描結束,將棧內剩餘運算符全部出棧並輸出 |
| 空 | - + 1 * + 2 3 4 5 | 空 | 逆綴輸出字元串 |
符號處理
對運算符的具體處理方法如下:
):直接入棧
(:遇)前,將運算符全部出棧並輸出;遇)後,將兩括弧一起刪除①
+、-:1
*、/、%:2
^:3
編程轉換
C++代碼
公式轉換
pascal代碼