標架叢
數學中， 標架叢（Frame bundle）是一個與任何向量叢 E相伴的主叢。F( E) 在一點 x的纖維是 E的所有有序基或曰標架。一般線性群通過基變更自然作用在 F( E) 上，給出標架叢一個主 GL( R)-叢結構，這裡 k是 E的秩。
一個光滑流形的標架叢是與其切叢相伴的叢。因此它有經常稱為 切標架叢（tangent frame bundle）。
定義與構造
設 E→ X是拓撲空間 X上一個 k階實向量叢。在點 x∈ X的一個 標架是向量空間 E的一個有序基。等價地，一個標架可以視為線性同構
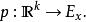切標架叢在 x的所有標架集合，記作 F，所有可逆 k× k矩陣組成的一般線性群GL( R) 在它上面有一個自然右作用：一個群元素 g∈ GL( R) 通過複合作用在 p的標架上給出一個新標架
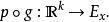切標架叢GL( R) 在 F上這個作用是自由傳遞的（這是標準線性代數結論：存在惟一可逆線性變換將一個基變為另一個）。作為一個拓撲空間 F同胚於 GL( R)，但它沒有群結構，因為沒有“優先的標架”。空間 F稱為一個 GL( R)-torsor。
E的 標架叢，記作 F( E) 或 F( E)，是所有 F的不交並：
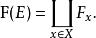切標架叢F( E) 中每個點是一個二元組 ( x, p)，其中 x是 X中一點而 p是 x處一個標架。存在自然投影 π: F( E) → X將 ( x, p) 送到 x。群 GL( R) 如上右作用在 F( E) 上。這個作用顯然是自由的且軌道恰是 π的纖維。
標架叢 F( E) 可給一個自然的拓撲，其叢結構由 E確定。設 ( U, φ) 是 E的一個局部平凡化。則對每個 x∈ U有一個線性同構 φ: E→ R。這個數據決定了一個雙射
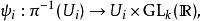切標架叢由下式給出
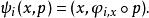切標架叢有了這個雙射後，每個 π( U) 可賦予 U× GL( R) 的拓撲。則 F( E) 上的拓撲是由包含映射 π( U) → F( E) 余誘導的最終拓撲。
有了上面所有數據後，標架叢 F( E) 成為 X上一個結構群為 GL( R) 的主纖維叢，具有局部平凡化 ({ U}, { ψ})，可以驗證 F( E) 的轉移函式與 E的相同。
上面所有工作對光滑範疇也成立：如果 E是光滑流形 M上一個光滑向量叢，則 E的標架叢可賦予 M上光滑主叢結構。
切標架叢
一個光滑流形 M的 切標架叢（或簡稱 標架叢）是與 M的切叢相伴的標架叢。 M的標架叢通常記作 F M或 GL( M) 而不是 F( TM)。如果 M是 n-維的則切叢的秩為 n，所以 M的標架叢是 M上一個主 GL( R) 叢。
光滑標架
M的標架叢的局部截面稱為 M上的光滑標架。主叢橫截定理說 M中任何有光滑標架的開集 U上標架叢是平凡的。給定一個光滑標架 s: U→ F U，平凡化 ψ: F U→ U× GL( R) 由
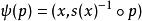切標架叢給出，這裡 p是 x處一個標架。從而一個流形是可平行化的若且唯若 M的標架叢有一個整體截面。
因為 M的切叢在 M的任何坐標鄰域是可平凡化的，故標架叢也是。事實上，給定任何坐標鄰域 U帶有坐標 ( x,…, x)，坐標向量場
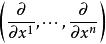切標架叢定義了 U上一個光滑標架。在標架叢上工作的一個好處是它們允許我們處理標架而不是坐標架；我們可選取對手中問題合適的標架。這有時稱為活動標架法。
焊接形式
流形 M的標架叢是一類特殊的主叢，它的幾何本質上繫於 M的幾何。這種關係可用 F M上一個稱之為 焊接形式（或稱 基本或 重言1-形式）向量值 1-形式表示。設 x是流形 M上一點， p是 x處一個標架，故
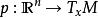切標架叢是 R與 M在 x處切叢的一個線性同構。F M的焊接形式是一個 R-值 1-形式 θ，定義為
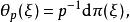切標架叢這裡 ξ與 F M相切於 ( x, p)， p:T M→ R是標架映射的逆，d π是投影映射 π: F M→ M的微分。焊接形式是水平的，它在與 π的纖維相切的向量上為零，以及右等變，即
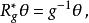切標架叢這裡 R是由 g∈ GL( R) 的左平移。F M上這樣性質的形式稱為基本或張量性形式。這樣的形式與 TM-值 1-形式一一對應，從而與 M上光滑叢映射 TM→ TM一一對應。這樣看來， θ恰好是 TM上恆等映射。
G-結構
參見：G-結構
如果光滑流形 M有額外的結構，通常自然地考慮 M全標架叢的一個適應於給定結構的子叢。例如，如果 M是一個黎曼流形，我們從上面看到自然地去考慮 M的標準正交標架叢。標準正交標架叢只不過是 F( M) 的結構群到正交群 O( n) 的約化。
一般地，如果 M是一個光滑 n-流形， G是 GL( R) 的一個子李群，我們定義 M上一個 G-結構為 F( M) 結構群到 G的一個約化。具體地說，這是 M上一個主 G-叢 F( M)，以及 M上一個 G-等變叢映射
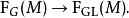切標架叢在這種語言中， M上一個黎曼度量給出 M上一個 O( n)-結構。下面是其它一些例子。
•每個定向流形有一個定向標架，這就是M上一個 GL(R)-結構。
•M上一個體積形式確定了M上一個 SL(R)-結構。
•一個 2n-維辛流形有一個自然的 Sp(R)-結構。
•一個 2n-維復或殆複流形有一個自然的 GL(C)-結構。
在某些例子中， M上一個 G-結構惟一確定了 M上對應的結構。例如 M上一個 SL( R)-結構確定了 M上一個體積形式。但是，在某些情形，比如辛與複流形，需要一個可積性條件。 M上一個 Sp( R)-結構惟一確定了 M上一個非退化2-形式，但對 M是辛的，這個 2-形式必須也是閉的。
