分維指標是分數維數（Fractal Dimension）基礎上算出的指標，請和分形指標區別開來，分維是用真正分維的數學定義進行計算來的，一般單純的下降線維數為1.0而複雜的線---比如盤整階段其線占了一個面且彎彎曲曲，所以維數可以升為1.1以上，按盤整程度強弱作分子除適當計算其它值並限制最後值在0.0到1.0之間變動就做成了分維指標(David Nichols的計算方法)。
指標直接相關參考連線和內容
“從 1.1到1.9分維越來越大,如果盤整明顯則分維指標值高,然後變盤後的趨勢越明顯,所以能構成市場延伸的測度.又因為分維指標計算和均線有共同短處,所以分維指標來不及稀釋,強趨勢時,往往要一跌再跌才達到0.35以下,趨勢終止也要慢慢等盤整度量比例加大才重回0.5一線。”
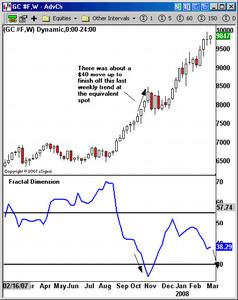黃金 分維指標“進入交易世界中經常令人迷惑不解的一個領域：隨機盤整趨勢。這種形態各異的盤整表現為一種動態的價格發展趨勢，相信有無數的投資者曾在這裡受過挫折，傷害。在這個階段，市場不斷誘導你犯錯誤，你沽出則可能漲；你進入則可能跌；你感覺風險很大時則可能大漲。在這個階段，所有的交易員幾乎都犯過無數的錯誤，這一切究竟是什麼原因？這裡看上去就像另一個星球，萬有引力等地球上所有的物理規律都不復存在，我可以肯定的告訴大家：這裡的確沒有任何規律可言。這也就是為什麼無數有志之士數百年來研究開發各種方法來預測股價趨勢而無法有效成功的原因！現在有一個分維指標至少可以隨時提醒我們這裡分維指標值高，就是盤整---小心！”
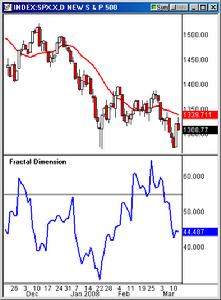SPX Fractal Dimension上段介紹的是David Nichols的計算方法。參見
http://www.321gold.com/editorials/nichols/nichols031408.html
圖片在下文圖Fractal Dimension 中還有。
另外一種是不用分子分母化為100%內的值，而是直接用維數，比如Radha Panini的分形維數計算值是直接用1到2之間的數字表示。大於1.5就是盤整，公式如下。
Fractal Dimension Index (FDI) 的圖片在圖FDI 中。
{Notes: March 2007 Issue - Using the Fractal Dimension Index - Trading Systems and Fractals by Radha Panini}
{vt_FDI Version 1.0}
Ri:= log(price/Ref(price,-1));
Mn:= sum(ri,periods)/periods;
X:= sum((Ri-Mn),periods);
Rn:= hhv(X,periods) - llv(X,periods);
Sn:= STDEV(Ri,periods);
Hurst:= log(Rn/Sn) / log(periods/2);
FDI:= 2 - Hurst;
http://www.traders.com/Documentation/FEEDbk_docs/Archive/042007/TradersTips/TradersTips.html
Radha Panini's March 2007 S&C article "Using The Fractal Dimension Index: Trading Systems And Fractals" builds on Erik Long's May 2003 S&C article, "Making Sense Of Fractals." In the March 2007 article, Panini shows how to use a fractal dimension index 。
圖片和解說
圖片
圖 Fractal Dimension
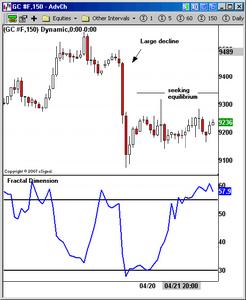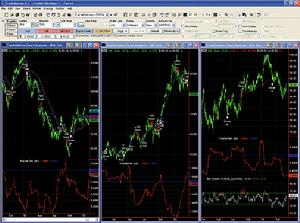分維指標圖 FDI
FDI附：分維的解釋
1.分形(Fractal)是指具有自相似特性的現象、圖像或者物理過
程等。分形學誕生於 1970年代中期，屬於現代數學中的一個分
支。分形學的創始人是具有法國和美國雙重國籍的曼德勃羅(就是波努瓦·芒德勃羅) ，
他在1982年出版的《大自然的分形幾何學》 （The Fractal
Geometry of Nature）是分形學的經典著作。 分形一般有以下
特質：
分形有無限精細的結構，即有任意小比例的細節
分形從傳統的幾何觀點看如此不規則，以至於難以用傳統的幾
何語言來描述
分形有統計的或近似的自相似的形式
分形可以由簡單的方法定義，例如疊代
分形的維數(可以有多種定義)大於其拓撲維數
2.分維反映分形的複雜性特點，通過計算可得分形的維數（分
維）值。
參考文獻
[1] Mandelbrot,B.B.,1967,How long is the coast of
Britain? Statistical selfsimilarity and fractional
dimension,Science,155,636~638
[2] Mandelbrot,B.B.,1977,Fractals,Form,Chance and
Dimension,San Francisco,W.H.Freeman&Co.
[3] Mandelbrot,B.B.,1982,The Fractal Geometry of
Nature,San Francisco,Freeman.
[4] 李水根，2004，分形，北京：高等教育出版社
