概念
分散式選擇算法
分散式選擇算法
分散式選擇算法
分散式選擇算法
分散式選擇算法 分散式選擇算法
分散式選擇算法分散式選擇算法是由通信連結的多個場點或節點協同完成某項任務的算法。在分散式選擇算法中，假定記錄元素都是分布在若干場點的局部存儲器中，各場點間可以任意形式的網際網路連線。一組進程的通信都經由固定的一組交換信息的通道C。通道的雙方都約定在一個傳送、另一個接收的規程上。令是一通信網路，其中是一組進程，是一組通道，輸入數據分布在各個進程中，因此分散式算法就是相對於和對問題的求解。
分散式選擇算法 分散式選擇算法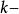 分散式選擇算法 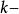分散式選擇算法 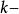分散式選擇算法通常所稱的選擇算法有兩種，一是隨機選擇1，二是確定選擇算法。前者平均複雜度為線性的，最壞複雜度為二次的；後者最壞複雜度為線性的。此兩種算法具有很多共同之處，差別僅在於劃分元素的選取方式不同，一個是隨機選取，另一個是按某一確定方式選取，從而分別名為隨機選擇和確定選擇。
工作原理
隨機k-選擇算法
（1）順序隨機k-選擇算法
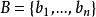分散式選擇算法令是元素的集合，欲從中選取第k個元素，則隨機k-選擇算法可描述如下：
1、如果|B|=1，則返回此元素；否則執行以下各步；
2、隨機從B中挑選一個元素m（以下稱其為劃分元素）；
3、將B劃分成是三個子集BL，BE，BG，它們分別包含<，=，>的那些元素。
4、遞歸調用本算法，以求出B'中的第k'個元素。
（2）分散式隨機k-選擇算法
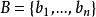分散式選擇算法
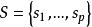分散式選擇算法Shrira等人於1983年曾將上述順序隨機k-選擇算法轉換成為分散式隨機k-選擇算法。另是元素集合，是場點集合可直截了當地轉換成分散式算法，對於遞歸部分只要由根節點協調好遞歸的入口和出口即可。
確定k-選擇算法
（1）順序確定k-選擇算法
1、如果|B|比較小（例如不大於50個元素），則可使用排序的方法求得第k個元素；否則執行以下各步；
2、將B按5個一組進行分組（至多有一組包含少於5個元素，稱此組為零頭）；
3、採用排序法求每組的中值，從而形成中值集合M；
4、自身遞歸調用，求集合M之中值m。
（2）分散式確定k-選擇算法
協調遞歸的入口和出口均在根部完成。根節點分布計算現有的活躍元素，如果所剩的不多，則根節點通知所有其他進程將這些元素髮送至根節點，然後由其求出第k個元素；如果仍有很多活躍元素，則根節點通知所有其他進程，於是它們都遞歸地調用局部的程式。
