函式空間S

簡介

函式空間S又為函式空間S(E)，是可測函式組成的函式類。

可以在測度空間上，類似的建立S空間。

定義

設E是R 內的勒貝格可測集，E上所有幾乎處處有限的可測函式之集記為S(E)，不強調E時簡記為S。

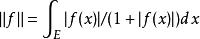函式空間S

對於f∈S(E)，令，則S(E)是以||・||為準範數的弗雷歇空間，且在其中依準範數的收斂等價於依測度收斂。可以在測度空間上，類似的建立S空間。

可測函式

設f是定義在可測集E上的實函式。如果對每一個實數，集E[f>a]恆可測（勒貝格可測），則稱f是定義在 E上的（勒貝格）可測函式。

設(X,F)為一可測空間，E是一個可測集。f: E→R*為定義在E上的函式。若對任意實數a，總有{x∈E: f(x)<a}∈F，則稱f為E上的F-可測函式（簡稱E上的可測函式）。

特別地，若可測空間取為是R 上的Lebesgue可測空間。E是R 中的Lebesgue可測集。則E上的可測函式成為Lebesgue可測函式。若可測空間取為R 上的Borel可測空間，E是R 中的Borel集，則E上的可測函式稱為Borel可測函式。