簡介
 冪級數
冪級數函式項級數的概念
定義1
設函式列u1(x),u2(x),u3(x),...,un(x),...都在區域I上有定義,則表達式
u1(x),u2(x),u3(x),...,un(x),...稱為定義在I上的函式項級數。
定義2
取x0屬於I,則函式項級數u1(x0),u2(x0),u3(x0),...,un(x0),...則稱為常數項級數。
若該常數項級數收斂,則稱x0為的收斂點;
若該常數項級數發散,則稱x0為的發散點。
定義3
函式項級數的收斂點全體的集合稱為其收斂域,發散點全體的集合稱為其發散域。
定義4
對於任意一點x,級數u1(x),u2(x),u3(x),...,un(x),...所確定的和應該是x的函式,記作:
s(x)=u1(x),u2(x),u3(x),...,un(x),...(x屬於I).
s(x)稱為定義在I上的和函式。
定義5
若用sn(x)表示函式項級數的前n項的和,
則在收斂域上有rn(x)=s-sn(x),rn(x)稱為餘項。
冪級數
冪級數的有關概念
定義6 具有下列形式的函式項級數
 冪級數
冪級數(1)稱為冪級數。
特別地,在中令即上述形式化為
(2)稱為 的冪級數。
取為常數項級數,如收斂,其和為
取為常數項級數,如收斂,其和為
取為和函式項級數,總收斂,其和為
對冪級數主要討論兩個問題:
(1)冪級數的收斂域 (2)將函式表示成冪級數。
冪級數的收斂域具有特別的結構
定理1:(i)如 在 收斂,則對於滿足 的一切 , 都絕對收斂;
(ii)如 在 發散,則對於滿足 的一切 , 發散。
證:(1)∵ 收斂
∴ (收斂數列必有界)
而 為幾何級數,當 即收
∴ 收 ∴ 原級數絕對收斂
(2)反證:如存在一點 使 收
則由(1) 收,矛盾。
由證明可知冪級數的收斂域為數軸上的對稱區間,因此存在非負數R,使 收斂; 發散,稱R為收斂半徑,(-R,R)為收斂區間。
冪級數的收斂域及其求法
定理2:如冪級數 係數滿足 ,
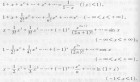 冪級數
冪級數則(1收斂區間為(-R,R);
(2)收斂區間為(-∞,+∞);
(3)冪級數 僅在一點x=0處收斂。
注意:當時, 的斂散性不能確定,要討論 的斂散性,從而求得收斂域。
例1:求下列冪級數的收斂域。
(1) (2) (3)
解:(1) , 故 ,
當 時, 原級數為 為交錯級數,滿足
¬ , ∴ 收斂;
當 時, 原級數為 發散,
∴ 收斂域為
解(2)由於 ∴ 故收斂域為 。
解(3)
令 ∴ 。
當 時,
原級數為
∴ 發散;
同理 時, 級數也發散 ,
∴收斂域
冪級數的性質
定理
求冪級數的和函式:利用逐項求導,逐次積分及四則運算等於將其化為可求和的形式,即化到公式:
冪級數的和函式
若對冪級數中的每一個x都有a0+a1x+a2x+…+anx+…=S(x),則稱S(x)為冪級數的和函式。