公理複雜性理論
正文
用公理方法研究部分遞歸函式的計算複雜性的理論。從空間、時間這樣具體的資源中抽象出一般性質，作為抽象資源必須滿足的公理。公理複雜性理論就是研究抽象資源耗費的複雜性。假設序列M1，M2,…枚舉了全部計算機器，Mi計算了部分遞歸函式φi(n),把滿足下面兩條公理的與 φi有關的遞歸函式Φi當作計算φi所消耗的抽象資源量。公理一：Φi(n)有定義，若且唯若φi(n)有定義。公理二：函式
顯然，時間、空間都滿足上述兩條公理，從這些公理出發可得出加速定理、間隙定理和壓縮定理。
① 加速定理：存在取值0，1的遞歸函式f，對f不存在計算它的最快的機器Mj。換言之，不論Mi對f的計算有多快,總可以找到另一台機器
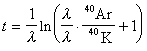，它比Mi能更快地計算f。這裡用“快”(或“慢”)來表示計算時消耗的資源量的少（或多）。 ② 間隙定理和壓縮定理：這是兩個相對立的結果，前者說明存在複雜度空穴：【h(n)，g(n，h(n))】(n＝1，2，…) 使任何Φi只進入有限次；後者說明Φi的密集性，即任給函式g(n，m)對每個i都有一li，使φ
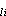的複雜度Φ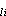(n)幾乎處處介於Φi(n)與g(n，Φi(n))之間。 這是一種早期理論，它使抽象複雜性的研究前進了一步，首次明確地提出資源耗費的問題，強調考慮和比對給定問題的一切可能的算法。另一方面由上述三條定理所反映的病態現象表明過於抽象的理論不能把握實用複雜性的本質。
