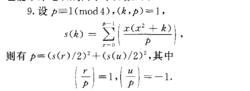相關結論
關於兩平方數之和定理有以下結論:
1.若n≡3(mod 4)，則n不能表示為兩平方數之和。
2.若n可表示為兩平方數之和，則對任一整數k，k n亦可表示為兩平方數之和。
3.n不能表示為兩平方數之和的充分必要條件是n的標準分解式中至少有一個素因數與3同餘(mod 4)且它的次數為奇數。
4.若p,q均可表示為兩平方數之和，則其乘積pq亦可表示為兩平方數之和。
5.任意素數x，若滿足x≡1(mod 4)，則可唯一地表示為兩平方數之和。
6.若n能表示為兩平方數之和，則n +1的每一個因數都能表示為兩個平方數的和。
7.設p是m的一個奇素因數，p能表示為兩平方數之和，若m能本原地表示成兩平方數之和，則m/p也能本原地表示為兩個平方數的和。
研究歷史
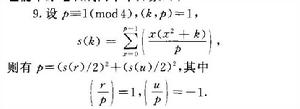兩平方數之和把一個自然數表示為兩平方數之和是數論中的一個古老問題。遠在公元3世紀末期，丟番圖(Dio-phantus)通過研究畢達哥拉斯三元數組後，已經知道如何把某些自然數表為二平方數之和，也知道形如4m+3的自然數不能表成二平方數之和。丟番圖將這些研究寫人了他早已失傳的《衍論》中，這些內容可從後人對該書的評註中見到.丟番圖的研究停留在算術階段，缺乏數論的特色。1640年12月25日，費馬(Fermat,P. de)給梅森(Mersenne, M.)的信中最先提出了形如4n+1的素數可以表成兩個平方數的和。1754年，歐拉(Eider, L.)首次證明了它，還證明了表達式的惟一性。
