概述
按普朗克 的說法,全同性有兩重意義,即相等性與不可分辨性。 Weisskopf曾經強調,全同性概念與量子化有本質的關係。此外,還應該提到量子統計物理的建立。 1924年,S.N.Bose用完全不同於經典的Maxwell-Boltzmann統計 法的一種涉及粒子全同性的新統計法,推導出了Planck的黑體輻射公式。後來量子力學建立後,Heisenberg、Fermi、Dirac等從量子態的置換反對稱性來說明Pauli不相容原理。對全同粒子的認識,許多人認為兩個粒子可以區分的。這種認識對經典粒子的區分性和全同粒子的不可區分性的錯誤看法。這種看法被解釋為只要是非定域的全同粒子都是不可分辨的,這似乎有問題,實際上不應該把分辨與不可分辨簡單地理解為能不能確定粒子的軌跡,而應該準確地理解為交換兩粒子的狀態,系統的微觀狀態是否變化,即全同性原理。
全同粒子的一般描述
在量子力學中,把屬於同一類的粒子稱為全同粒子,也就是說固有性質(質量、電荷、自旋、同位旋、宇稱、奇異數等)相同的粒子稱為全同粒子。粒子全同性概念與粒子態的量子化有本質的聯繫。如果沒有態的量子化概念,就沒有全同性概念的產生。在經典力學中,由於粒子的性質和狀態(質量、形狀、大小等)可以連續變化,巨觀角度上說明不了兩個粒子真正全同。在量子力學中,由於態的量子化,兩個量子態要么完全相同,要么完全不相同,中間無連續過渡。例如:兩個銀原子,不管它們是經過什麼工藝過程製備出來,通常條件下都處於基態,都用相同的量子態來描述,所以,我們說它們是全同的。
經典粒子的區分性與全同粒子的不可區分性
經典粒子和全同粒子
粒子的全同性對經典力學並無重大影響。經典力學中每個粒子有自己的位置, 可以按起始位置的不同區分它們。如稱t=0 時在A 處的粒子為第一個粒子, 在B 處的粒子為第二個粒子如圖1 (a)所示。每個粒子各沿自己的軌道運動,可用牛頓方程從起始狀態算出它們在任何時刻的狀態; 也可用牛頓方程算出找到的粒子起始時的位置從而認出它是哪個粒子,因此,經典力學性質的全同並不使每個粒子喪失個性, 全同粒子系中每個粒子仍有自己的狀態和獨立的運動過程, 交換兩個全同粒子將導致系統狀態的改變。
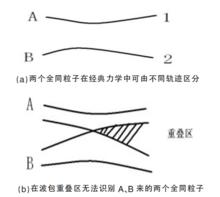 圖1 經典粒子的區分性和全同粒子的不可區分性
圖1 經典粒子的區分性和全同粒子的不可區分性在量子力學中情況根本不同, 波動性是軌道概念不適用,即使起始時每個粒子的狀態由波包描述從而有近似一定的位置,但隨後波包會擴散並且各粒子波包可能彼此重疊如圖1(b)所示。原則上無法判斷波包重疊的區域內找到的一個粒子原來屬於哪個波包,處在哪個位置。
假設與結論
全同粒子的不可分辨性,一般被解釋為波函式的重疊,由於波函式可以給出粒子的幾率分布,如果兩個全同粒子的波函式發生重疊,粒子就不可分辨了,這樣的解釋似乎是很自然的,但是仔細分析就會發現問題。假想在一個容器中有兩個沒有相互作用的全同粒子,這是一個非定域問題,假設兩個粒子同時逐漸變大,從微觀粒子變成巨觀粒子,那么它們就從不可分辨變成可分辨的了。
由於交換兩個非定域系統的全同粒子從整體上看不出來的,熵是混亂程度,這意味著混亂程度相同,即熵相同。因此,系統的微觀狀態應該從整體上即從巨觀上考慮,交換兩個非定域系統的全同粒子, 系統的微觀狀態不變。經典力學中,兩物體性質相同時,仍然可以區分,因各自有確定軌道。微觀粒子體系,因為運動具有波粒二象性,無確定軌道,在位置幾率重疊處就不能區分是哪個粒子。
以上討論可以得出:由於全同粒子的不可區分性,在全同粒子所組成的系統中,任意兩個全同粒子相互交換(位置等),不會引起系統狀態的改變。這就是全同粒子必須服從的全同性原理。
交換對稱性與全同性原理的關係
 全同性原理
全同性原理對全同粒子體系的波函式引入交換算符 ,它的作用是把波函式中的第i 個粒子和第j 個粒子的坐標交換位置:
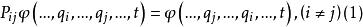 全同性原理
全同性原理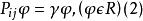 全同性原理
全同性原理那么全同性原理告訴我們,這樣交換以後的狀態與原來的狀態是不可區別的,所以,按照量子力學的基本原理 ,而
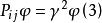 全同性原理
全同性原理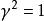 全同性原理
全同性原理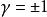 全同性原理
全同性原理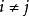 全同性原理
全同性原理所以 ,即 (對任意的 ).
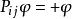 全同性原理
全同性原理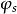 全同性原理
全同性原理若 ,則稱 為交換對稱波函式;(4)
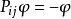 全同性原理
全同性原理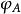 全同性原理
全同性原理若 ,則稱 為交換反對稱波函式;(5)
交換對稱性或反對稱性是全同粒子體系波函式特殊的固有的性質,因此也是(微觀)粒子特殊的、固有的性質。它決定了粒子所服從的統計。由(4)式和(5)可以看出描寫全同粒子體系狀態的波函式只能是對稱的或反對稱的,它們的對稱性不隨時間改變。這一點可以從全同粒子體系的哈密頓算符是粒子交換下不變的這點出發,很易得到證明。全同粒子體系的哈密頓算符是粒子交換不變,同樣可以證明全同粒子體系的反對稱波函式的反對稱性不隨時間改變。
量子力學中全同性原理的限制
為了說明全同性原理對統計產生的影響 ,討論同時投兩枚分幣的問題,每個分幣有兩面,代表兩種可能的狀態,分別以+ ,-表示。沒有全同性原理的限制, 系統可能的狀態總共有4 種,見表1。
表 1 系統可能的狀態
| 狀態數 | 第一次投幣 | 第二次投幣 |
| 1 | + | + |
| 2 | + | - |
| 3 | - | + |
| 4 | - | - |
每種出現的機率為1/4。如有一個分幣為+ ,有一個分幣為- 的機率則為1/2。這相當於經典力學的情形。在量子力學中,由於全同性原理,可能態的數目將減小。對於費米子, 由於反對稱的要求, 系統只能處於+ -和 - + 的態。++、- -及+ -和+-都不存在。也就是說,由於泡利原理的限制,系統只有一種可能狀態。而且在這一狀態中,我們不能指出哪一個分幣為+,哪一個分幣為- 。對於玻色子,可能的狀態是:+ + 、- - 、+ - 和- + ,每種出現的機率為1/3。由此看到,由於交換不變性,玻色子出現在不同態上的機率減少,出現在相同態的機率增加,這一現象稱為愛因斯坦凝聚。因此由於全同性原理的限制,一個統計結果可能有多種結論。
全同性原理說明
每類全同粒子有一種確定的對稱性,且這種對稱性不隨時間改變。因此,對稱性質本身也成了標誌一類全同粒子的屬性。在描述一種全同粒子性質時,除了列舉它們的電荷、質量等屬性外還可列舉它們的交換對稱性。一個全同粒子系的運動狀態波函式不僅要求遵從這個體系的薛丁格方程,而且必須具有相應的粒子交換對稱性。由於全同粒子具有交換對稱性,可以說系統的狀態不因交換兩個全同粒子而改變,所以,全同性原理是任何全同粒子系統必須遵從的、量子力學的第一原理。
