正文
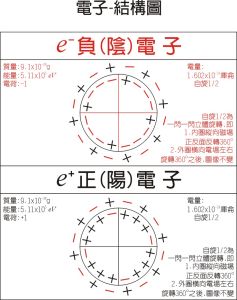電子-內部結構模型圖
。 全同粒子的存在是客觀物質世界的一項基本實驗事實,也是被物理學界所普遍接受的一項基本理論信念。仍以電子的電荷為例,雖然實驗測量受到精確度的限制,而且各次測量結果在最後幾位有效數字上有出入，但是當前絕大多數物理學家仍一致相信，所有電子（包括未被測量過的電子）的電荷值應該完全相同，沒有絲毫差別。任何物理理論，尤其是量子理論，都是在這種信念的基礎上建立起來的。
一個由若干個全同粒子組成的物理體系，其運動狀態的全部性質原則上應該可以由外部的"觀測者"（例如其他基本粒子）通過同這個體系的相互作用而一一查明。假如交換體系中任意兩個粒子（第i個和第j個）的運動狀況，因為實行交換的粒子是全同的，外界"觀測者"的觀測結果顯然不會受到任何影響，所以必須認為粒子i和j實行交換後體系仍處於同一運動狀態。這個觀點以及下面說的波函式具有交換對稱性或反對稱性通常稱為全同性原理。如以Ψ 表示交換前描述體系狀態的波函式。pijΨ 表示交換後體系的波函式，Ψ和pijΨ 既然描述同一狀態，它們最多相差一個常數因子。由於接連交換兩次波函式必須還原，這個常數因子只能是±1。當pijΨ＝+Ψ,就稱體系狀態為交換對稱的；當pijΨ＝-Ψ，則稱為交換反對稱的。
實驗表明，全同粒子體系狀態的交換對稱性，取決於粒子的自鏇，凡是自鏇等於媡整數倍 (0,媡,2媡)...的全同粒子系，波涵數是交換對稱的,並遵守玻色-愛因斯坦統計法則,這類粒子稱為玻色子。自鏇等於媡的半整數倍(媡/2,3媡/2,...) 的全同粒子系，波函式是交換反對稱的，並遵守費密-狄喇克統計法則,這類粒子稱為費密子。光子（自鏇為媡）、α粒子（自鏇為 0）、π介子(自鏇為0)則是玻色子；電子、質子、中子(自鏇均為 媡/2)是費密子。
π介子、質子、中子-內部結構模型表 對於全同費密子體系，體系中不能有兩個或兩個以上粒子同時處於相同的單粒子態。即每一個單粒子態最多只能容納一個粒子。這個結論習慣上稱為泡利不相容原理，是奧地利物理學家W.泡利(1925)為了解釋化學元素周期性而首先假設的，量子力學出現後，在全同性原理的基礎上從理論上證明了這一原理。泡利原理是原子、分子以及原子核結構的理論基礎之一。
玻色子體系不受泡利原理的限制，而且，由於粒子總是自發地向低能級躍遷，玻色子有向基態能級凝聚的傾向，這是產生低溫超導和超流現象的基本原因。
