公式定義
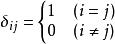克羅內克方法。
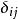克羅內克方法克羅內克函式的值一般簡寫為 。
克羅內克函式和狄拉克δ函式都使用δ作為符號，但是克羅內克δ用的時候帶兩個下標，而狄拉克δ函式則只有一個變數。
其它記法
另一種標記方法是使用艾佛森括弧（得名於肯尼斯·艾佛森）：
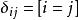克羅內克方法。
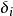克羅內克方法同時，當一個變數為0時，常常會被略去，記號變為 ：
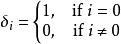克羅內克方法。
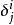克羅內克方法線上性代數中，克羅內克函式可以被看做一個張量，寫作 。
數位訊號處理
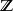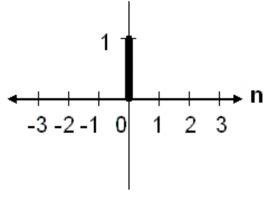
克羅內克方法類似的，在數位訊號處理中，與克羅內克函式等價的概念是變數為 (整數)的函式：
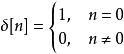克羅內克方法。
這個函式代表著一個衝激或單位衝激。當一個數字處理單元的輸入為單位衝激時，輸出的函式被稱為此單元的衝激回響。
性質
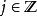克羅內克方法克羅內克函式有篩選性：對任意 ：
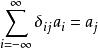克羅內克方法。
如果將整數看做一個裝備了計數測度的測度空間，那么這個性質和狄拉克δ函式的定義是一樣的：
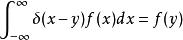克羅內克方法。
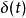克羅內克方法實際上，狄拉克δ函式是根據克羅內克函式而得名的。在信號處理中，兩者是同一個概念在不同的上下文中的表現。一般設定 為連續的情況（狄拉克函式） ，而使用 i, j, k, l, m, and n等變數一般是在 離散的情況下（克羅內克函式）。
線性代數中的套用
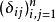克羅內克方法線上性代數中，單位矩陣可以寫作 。
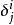克羅內克方法在看做是張量時（克羅內克張量），可以寫作 。
這個(1,1)向量表示:
作為線性映射的單位矩陣。
跡數。
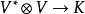克羅內克方法內積。
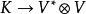克羅內克方法映射 ，將數量乘積表示為外積的形式。
廣義克羅內克函式
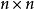克羅內克方法定義 廣義克羅內克函式為 矩陣的行列式，以方程式表達為
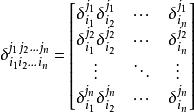克羅內克方法；
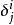克羅內克方法
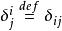克羅內克方法其中， 是個張量函式，定義為 。
以下列出涉及廣義克羅內克函式的一些恆等式：
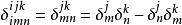克羅內克方法。
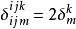克羅內克方法。
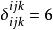克羅內克方法。
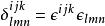克羅內克方法；
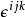克羅內克方法
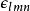克羅內克方法其中，和是列維-奇維塔符號。
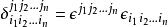克羅內克方法。
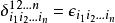克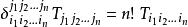羅內克方法。
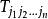克羅內克方法；
克羅內克方法
克羅內克方法其中，是階張量。
積分表示
克羅內克方法對任意的整數，運用標準的留數計算，可以將克羅內克函式表示成積分的形式：
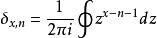克羅內克方法；
其中積分的路徑是圍繞零點逆時針進行。
這個表示方式與下面的另一形式等價：
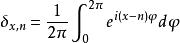克羅內克方法。
