克勒流形

克勒流形是一類重要的複流形，具有克勒度量的複流形稱為克勒流形。例如，C中有界域關於伯格曼度量為克勒流形。

簡介

克勒流形是一類重要的複流形。

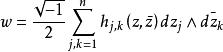克勒流形

設M有埃爾米特度量h，它對應一個(1,1)型外微分形式 稱為h的伴隨克勒形式。當dw=0時，h稱為克勒度量。具有克勒度量的複流形稱為克勒流形。

例如，C中有界域關於伯格曼度量為克勒流形。

克勒度量

克勒度量是特殊的埃爾米特度量。

設M是具有殆復結構J的殆複流形，g為M上的埃爾米特度量，Φ是相應的克勒形式，若Φ是閉的，即dΦ=0，則稱g為克勒度量。給定克勒度量的複流形，就稱為克勒流形。

複流形

在數學中，特別是在微分幾何和代數幾何中，複流形是具有復結構的微分流形，即它能被一族坐標鄰域所覆蓋，其中每個坐標鄰域能與n維複線性空間中的一個開集同胚，從而使坐標區域中的點具有復坐標 (z,…,z)，而對兩個坐標鄰域的重疊部分中的點，其對應的兩套復坐標之間的坐標變換是全純的。稱n為此複流形的復維數。

一個n維複流形也是2n維的（實）微分流形。