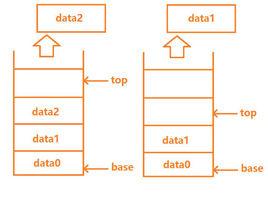
定義
棧（Stack）是限定僅在表尾進行插入或刪除操作的線性表。即棧的修改是按照後進先出的原則進行的，故棧又成為後進先出（Last In First Out）的線性表或先入後出佇列。
基本算法
進棧算法
①若TOP≥n時，則給出溢出信息，作出錯處理（進棧前首先檢查棧是否已滿，滿則溢出；不滿則作②）；
②置TOP=TOP+1（棧指針加1，指向進棧地址）；
③S(TOP)=X，結束（X為新進棧的元素）；
退棧算法
①若TOP≤0，則給出下溢信息，作出錯處理(退棧前先檢查是否已為空棧， 空則下溢；不空則作②)；
②X=S(TOP)，（退棧後的元素賦給X）；
③TOP=TOP-1，結束（棧指針減1，指向棧頂）。
代碼實現
C/C++
C語言或C++語言實現先進後出佇列（可不加鎖），舉例代碼如下：
Python
Queue是python標準庫中的執行緒安全的佇列實現,提供了一個適用於多執行緒編程的先進先出的數據結構，即佇列，用來在生產者和消費者執行緒之間的信息傳遞。Python內置四種佇列：LILO佇列，LIFO佇列，優先佇列和雙端佇列。LIFO佇列，即先入後出佇列，舉例代碼如下：
套用舉例
數制轉換
十進制數 N和其他 d進制數的轉換是計算機實現計算的基本問題，基本算法基於下列原理：
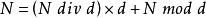先入後出佇列其中， div為整除運算， mod為求余運算。下面舉例實現將輸入的十進制數轉換成對應的八進制數：
括弧匹配的檢驗
在算法中設定一個棧，每讀入一個括弧，若是右括弧，那么有兩種結果：①使置於棧頂的最急迫的期待得以消除；②不合法。若為左括弧，則作為一個新的更急迫的期待壓入棧中，使得原有的在棧中的所以未消除的期待的急迫性下降一級。另外，在算法開始和結束時，棧都應該是空棧。 下面舉例實現括弧匹配的檢測：
