基本思想
先來先服務的調度算法:最簡單的調度算法,既可以用於作業調度 ,也可以用於程式調度,當作業調度中採用該算法時,系統將按照作業到達的先後次序來進行調度,優先從後備佇列中,選擇一個或多個位於佇列頭部的作業,把他們調入記憶體,分配所需資源、創建進程,然後放入“就緒佇列”,直到該進程運行到完成或發生某事件堵塞後,進程調度程式才將處理機分配給其他進程。
關鍵要領
按照進程進入就緒佇列的先後順序調度並分配處理機執行。先來先服務調度算法是一種非搶占式的算法,先進入就緒佇列的進程,先分配處理機運行。一旦一個進程占有了處理機,它就一直運行下去,直到該進程完成工作或者因為等待某事件發生而不能繼續運行時才釋放處理機。
(1)系統只要有按FIFO規則建立的後備作業佇列或就緒進程佇列即可,就是一個作業控制塊JCB或進程控制塊PCB加入佇列時加在相應佇列末尾。
(2)調度退出佇列時從相應佇列首開始順序掃描,將相關的JCB或PCB調度移出相應佇列。
系統模型
設處理機或系統資源為伺服器,一個進程或一個作業為享受該伺服器服務的顧客.這些顧客按 FCFS 方式排隊享受服務的系統模型為:
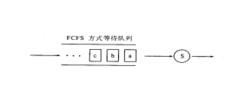 先來先服務
先來先服務這裡 ,我們假定該系統模型中只有一個伺服器 S.設新顧客到達等待佇列的時間與系統的當前狀態、以前的顧客到達時間都無關,也就是新顧客到達系統的時間是服從泊松分布的.同時設伺服器 S為顧客提供服務的機率也服從泊松分布.
回響時間計算
(1) 單位時間顧客到達的平均值和顧客被服務的平均值
因顧客到達系統的時間服從泊松分布,設 λ為到達率 ,
單位時間內顧客到達的期望值 ,即算術平均值為 :
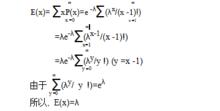 先來先服務
先來先服務即單位時間內顧客到達的平均值等於其到達率 .
同理,被伺服器 S服務的顧客個數的平均值也等於其服務率 .
(2)兩個連續到達的顧客之間的平均時間間隔和伺服器服務時間的平均值
將上述單位時間換成任意時間 t,可得到在已知時間 t內 x個顧客到達的機率,從而 ,t時間內至少到達一個顧客的機率也可知。
如果把時間 t看成是固定的時間間隔 ,則有在任何時間間隔 t內至少有一個顧客到達的機率和t時間內至少到達一個顧客的機率相等,這個機率和上一次顧客到達的時刻無關,這個特性稱為無記憶特性或馬爾可夫性質.
根據機率P(x) , 可知其密度函式和t 的期望值。
即兩個連續到達的顧客之間的平均時間間隔為 1/ λ.同理,可得伺服器服務時間的平均值為1/ μ.顯然,只有當 1/ μ<1/ λ也就是λ<μ時系統才是穩定的.否則,等待服務佇列將無限增長 .
(3)系統在穩定狀態下回響時間的計算
設 Si為系統的一個狀態,表示等待服務的佇列中有 i-1個顧客,伺服器中有 1個顧客存在.再設系統在 t時間內處於狀態Si的機率為Pi(t).
系統在穩定狀態下,系統內不存在顧客的機率為 1 -ρ,而系統記憶體在顧客的機率為ρ.系統內顧客的算術平均值是:
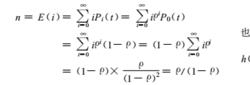 先來先服務
先來先服務上述按FCFS方式排列和調度 ,並只有一個伺服器的系統稱為M/M/1系統 .第一個字母M表示顧客到達時間間隔是指數分布 ,具有馬爾可夫性質 ,第二個字母 M表示從伺服器離開的顧客的時間間隔服從指數分布 ,具有馬爾可夫性質 ,第三個數字 1表示只有一個伺服器.
設回響時間 R為從顧客到達等待佇列後開始到離開伺服器的時間.系統進入穩定狀態之後 ,系統中的顧客數 n和平均回響時間 R 之間存在一個非常簡單的關係:n =λR , λ為顧客的平均到達率.可以求出M/M/1系統的平均回響時間為:
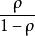 先來先服務
先來先服務R=n/λ= ·(1/λ)=1/μ(1-ρ)
由此可以看出 ,M/M/1系統的服務性能是由 ρ決定的.如果 ρ趨近 1,即 λ趨近 μ,則回響時間急劇增大 ,系統性能變差.而當 ρ小於 1/2時 ,等待佇列中為空的可能性較大 ,因為平均回響時間小於平均服務時間的2倍 .
對短作業影響
設短作業的到達率和服務率分別為(λ1, μ1),長作業的到達率和服務率為(λ2, μ2),且兩者都服從泊松分布 ,則 二者的合成仍是泊松過程 ,
一般來說,短作業的服務時間1/μ1遠小於長作業1/μ2,先來先服務調度策略的回響時間R為:
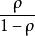 先來先服務
先來先服務R=n/λ=·(1/λ)=1/μ(1-ρ),其中λ=λ1+λ2,μ=μ1+μ2.
由於 λ和ρ中包含了λ1, λ2, μ1, μ2,所有作業的平均回響時間相同 ,從而,短作業在系統中的駐留平均時間與長作業的駐留平均時間相同 , 這對短作業是不利的.
優缺點
有利於長作業(進程)而不利於短作業(進程)
有利於CPU繁忙型作業(進程)而不利於I/O繁忙型作業(進程)

