簡介
韋格納分布（Wigner Distribution Function，WDF）是由1963年的諾貝爾物理學獎得主尤金·維格納，於1932年首次引用的一個新的方程式。一種時頻混和的信號表示法，能同時進行時域和頻域分析，並把兩者結合起來，其各階矩具有明確的物理意義，其特有的性質很適合腦電信號的特徵提取。
眾所皆知，傅立葉變換對於研究穩態(時間獨立)的訊號(波形)是一項非常有用的工具，然而，訊號(波形)一般來說在時間上並非是獨立的，這樣的訊號或是波形傅立葉變換並無法有效地完全分析其特性，因此對於一個非穩態的訊號完全分析需要測量出時間以及頻率上的表現。偽韋格納分布是韋格納分布一個變種，定義如下：
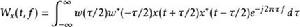偽韋格納分布偽韋格納分布對頻率方向實現了平滑，因此保留的是時間集中的韋格納分布，不能減少干擾項的震盪。
平滑偽韋格納分布
上平滑偽韋格納分布(smoothed pseudo-Wigner distribution,SPWD)是一個有平滑時間方向的偽韋格納分布。平滑偽韋格納分布允許簡單且有彈性的選擇平滑特性以及執行效率。但如同短時傅立葉變換的絕對值平方(spectrogram)，它不符合大多數數學特性滿意的韋格納分布（意即:不符合大多數的理想數學特性，如邊際(marginal)或有限的支持(finite-support)特性）。
平滑偽韋格納分布(SPWD)定義為時間平滑短時(time-smoothed short-time)的偽韋格納分布，其運行分析視窗為h(t)和一個時間平滑視窗g(t)。平滑偽韋格納分布在模糊域(ambiguity-domain)的權重函式(weighting function)為
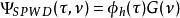偽韋格納分布
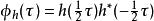偽韋格納分布，
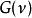偽韋格納分布
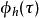偽韋格納分布 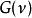偽韋格納分布是對g(t)做傅立葉變換。權重函式是一個可分解的函式，分解成 和 ，各別相依於分析視窗h(t)和時間平滑視窗g(t)。
藉由分別適當選擇視窗g(t)以及h(t)的長度，使得大量的時間平滑與頻率平滑能夠容易的控制: 一個較長的g(t)產生更多的時間平滑和一個較長的h(t)產生較少的頻率平滑。對於一般視窗g(t)和h(t)，平滑偽韋格納分布對應於一個非常簡單的二維低通濾波器。權重函式 {\displaystyle \Psi _{SPWD}(\tau ,\nu )}通常類似一個二維的高斯函式(Gaussian function)，由於形狀簡單的權重函式，平滑偽韋格納分布的干擾項衰減和時頻集中，將不會過於依賴詳細的時頻信號結構下的分析。
優缺點
優點 ：
1.有良好的解析度，尤其是對單一成分，且瞬時頻率變化不為2次式以上。
2.有好的數學運算性質。
3.可用於分析隨機程式。
缺點 ：
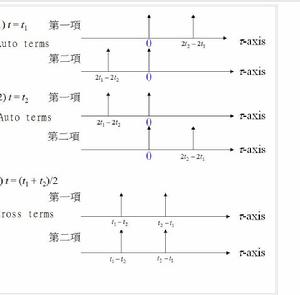
1.有相交項(cross term)的問題，改進方法請見 改進型韋格納分布。
2.需要更多的時間去計算，若訊號時間越長，則需要更久的時間。
3.不是一對一函式，無法辨別相位部分。
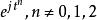偽韋格納分布4.不適合分析瞬時頻率變化為2次式以上的型態，即 。
