簡介
倍邊公式是求正多邊形邊長的公式。
由正 n 邊形邊長 a 求同半徑 R 的正 2n 邊形的邊長 a 的公式為
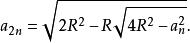 倍邊公式
倍邊公式倍邊公式曾被中外古代數學家用於計算圓周率的近似值。
簡化形式
在求邊數倍增的圓內接正多邊形的邊長時,很少運用現成的倍邊公式。
高中平面幾何課本中關於圓內接正多邊形的倍邊公式是這樣給出的:
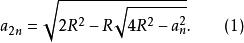 倍邊公式
倍邊公式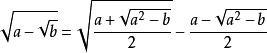 倍邊公式
倍邊公式如果將(1)式根據代數上所講的公式進行變換,可變
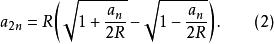 倍邊公式
倍邊公式(2)式和(1)式比較起來,不但形式簡單,便於記憶;而且由於(2)式比(1)式少了一層開方運算,也容計算,並且精確度更易較高,例如求半徑是 R 的圓的內接正 12 邊形的邊長。
利用上面兩張方法進行計算,結果是這樣(精確度為10 ):
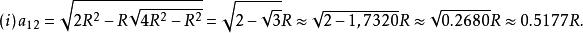 倍邊公式
倍邊公式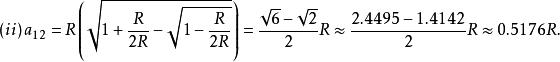 倍邊公式
倍邊公式事實上,(ii) 的結果比較接近真值 R×0.51762...。
