定義
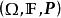 保測變換
保測變換設是一(完備)機率空間。
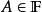 保測變換
保測變換定義1 如果對於任何,有
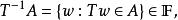 保測變換
保測變換 保測變換
保測變換 保測變換
保測變換則空間到自身的影射稱做 可測的。
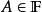 保測變換
保測變換定義2 如果對於任何,有
 保測變換
保測變換 保測變換
保測變換則可測影射稱做 保測變換(morphism)。
 保測變換
保測變換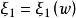 保測變換
保測變換 保測變換
保測變換 保測變換
保測變換設T是保測變換,是其n次冪,而是一隨機變數,設,考慮序列。
保測變換舉例
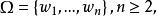 保測變換
保測變換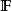 保測變換
保測變換 保測變換
保測變換 保測變換
保測變換 保測變換
保測變換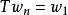 保測變換
保測變換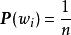 保測變換
保測變換 保測變換
保測變換例1 設是由有限個點構成的集合,是中一切子集的代數,,而.如果,則是保測變換。
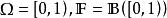 保測變換
保測變換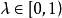 保測變換
保測變換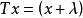 保測變換
保測變換例2 設, P是勒貝格測度,,則是保測變換。
保測變換的物理前提條件
 保測變換
保測變換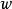 保測變換
保測變換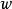 保測變換
保測變換 保測變換
保測變換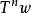 保測變換
保測變換 保測變換
保測變換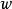 保測變換
保測變換 保測變換
保測變換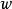 保測變換
保測變換 保測變換
保測變換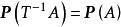 保測變換
保測變換 保測變換
保測變換假設某一系統按照一定運動規律(在離散時間)演變,並構想是該系統的狀態的相空間,那么,如果是系統在時刻的狀態,則是經過n步系統進入的狀態,其中是(該運動規律誘導的)推移運算元,其次,假如A是某一“狀態的集合”,則根據其定義是經一步到達集合A的一切“初始”狀態的集合,因此,假如把視為“不可壓縮的液體”,則條件可以視為完全自然的“體積”保持不變的條件。(對於經典的封閉哈密頓(W.R.Hamilton)系統,著名的劉維爾(J.Liouville)定理斷定,相應的變換是保持勒貝格測度不變的變換。)
關於保測變換的龐加萊定理
下面關於“常返性”的龐加萊(J.H.Poincaré)定理(1912),是有關保測變換最早的成果之一。
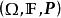 保測變換
保測變換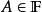 保測變換
保測變換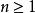 保測變換
保測變換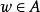 保測變換
保測變換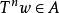 保測變換
保測變換定理 設是一機率空間, T是保測變換,.那么,對於無限多個和幾乎一切點,有。
 保測變換
保測變換 保測變換
保測變換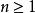 保測變換
保測變換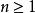 保測變換
保測變換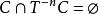 保測變換
保測變換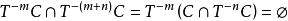 保測變換
保測變換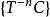 保測變換
保測變換證明: 記={,對於一切).由於對於任意,,則,這樣,序列由有相同 P一測度的不相交集合構成,因此,
 保測變換
保測變換 保測變換
保測變換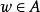 保測變換
保測變換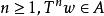 保測變換
保測變換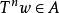 保測變換
保測變換從而。從而,對於幾乎一切點和至少對於一個,由此可見,對於無限個n≥1,有。
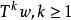 保測變換
保測變換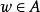 保測變換
保測變換 保測變換
保測變換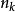 保測變換
保測變換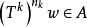 保測變換
保測變換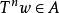 保測變換
保測變換將上面得到的結果用於變換,那么,對於每一個點\,其中 N是0機率集合(並且 N是對應於不同 k的相應集合的並),存在這樣的,使.由此顯然可以得到,對於無限多個n,有。
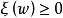 保測變換
保測變換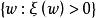 保測變換
保測變換設,則在集合上
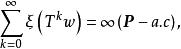 保測變換
保測變換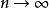 保測變換
保測變換如果令當時,得所要證明的結果。
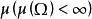 保測變換
保測變換注: 假如將機率測度 P換成任意有限測度,則定理仍然成立。