概念
 伯德圖
伯德圖伯德圖是線性非時變系統的傳遞函式對頻率的半對數坐標圖,其橫軸頻率以對數尺度(logscale)表示,縱坐標幅值或相角採用線性分度,利用伯德圖可以看出系統的頻率回響。伯德圖一般是由二張圖組合而成,伯德圖由兩張圖組成:①G(jω)的幅值(以分貝,dB表示)-頻率(以對數標度)對數坐標圖,其上畫有對數幅頻曲線;②G(jω)的相角-頻率(以對數標度)對數坐標圖,其上畫有相頻曲線。
對數幅值的標準表達式為20lg|G(jω)|,單位是分貝,相角的單位是度。由於增益用對數來表示(log(ab)=log(a)+log(b)),因此一傳遞函式乘以一常數,在伯德增益圖只需將圖形的縱向移動即可,二傳遞函式的相乘,在波德幅頻圖就變成圖形的相加。幅頻圖縱軸0分貝以下具有正增益裕度、屬穩定區,反之屬不穩定區。
配合波德相頻圖可以估算一信號進入系統後,輸出信號及原始信號的比例關係及相位。例如一個Asin(ωt)的信號進入系統後振幅變原來的k倍,相位落後原信號Φ,則其輸出信號則為(Ak)sin(ωt−Φ),其中的k和Φ都是頻率的函式。相頻圖縱軸-180度以上具有正相位裕度、屬穩定區,反之屬不穩定區。
分析過程
繪製伯德圖的一般步驟為:首先將開環頻率特性G(jω)H(jω)改寫為基本環節的乘積,畫出各基本環節的伯德圖,然後把各基本環節伯德圖的對數幅值相加,相角相加,就得到G(jω)H(jω)的伯德圖.得到伯德圖後,對其進行一定的分析,就可以得到系統的穩定特性等。分解為典型環節
系統開環傳遞函式由八種典型環節構成,將任意開環傳遞函式的分子、分母進行因式分解,都可以將開環傳遞函式轉化為若干典型環節的乘積,這八種典型環節為:
比例環節K;
慣性環節(Ts+1)-1(T>0);
一階微分環節Ts+1(T>0);
積分環節s-1;
微分環節s;
振盪環節ωn2/(s2+2ζωns+ωn2),(ωn>0,0<ζ<1);
二階微分環節(s/ωn)2+2ζs/ωn+1(ωn>0,0<ζ<1);
延遲環節eτs.
具體計算過程如下:
頻率特性可以寫成一般的形式
式中K為增益(放大係數),ωn為無阻尼自然頻率,ζ為阻尼比。
頻率特性的對數幅值(使用記號Lm)表達式為(公式2)
頻率特性的相角表達式為(公式3)
或(公式4)
伯德圖畫法
畫伯德圖時,分三個頻段進行,先畫幅頻特性,順序是中頻段、低頻段和高頻段。將三個頻段的頻率特性(或稱頻率回響)合起來就是全頻段的幅頻特性,然後再根據幅頻特性畫出相應的相頻特性來。
作伯德圖時,首先寫出頻率特性,然後按常數因子K、積分和微分因子(jω)、一階因子(1+jωT)和二階因子[1+2ζ(jω/ωn)+(jω)/ω]1這樣四種基本因子分別畫出伯德圖,再總加而成。
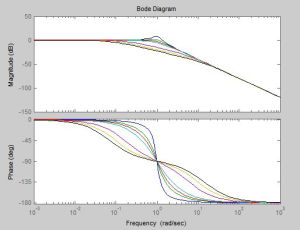
圖2、圖3是常見簡易傳遞函式的伯德圖趨勢。
分析方法
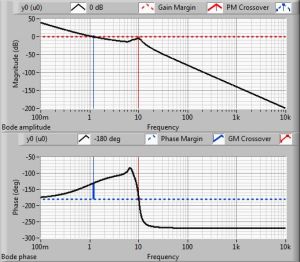
伯德圖可用來計算負反饋系統的增益裕度(gainmargin)及相位裕度,進而確認系統的穩定性。
相關符號定義
先定義以下的符號:
其中:
AFB是考慮反饋時的放大器增益(閉環增益)
β是反饋係數
AOL是不考慮反饋時的放大器增益(開環增益)。
在開環增益AOL遠大於1時,閉環增益AFB可以用以下方式近似
在開環增益AOL遠小於1時,閉環增益AFB可以用以下方式近似
增益AOL是頻率的複變函數,有大小及相位。
上述的式子中,若βAOL乘積=−1時,可能會出現增益無窮大(即為不穩定)的情形。(若用大小和相位來表示,此時βAOL的大小為1,相位為-180度,此條件即稱為巴克豪森穩定性準則。配合波德圖,不但可以判斷系統是否穩定,也可以判斷系統接近以上不穩定條件的程度。
在判斷系統穩定性時,會用到以下二個頻率。第一個頻率f180是上述乘積相位恰為-180度的頻率,第二個頻率f0dB則為乘積的絕對值|βAOL|=1時的頻率(若以分貝表示時,則為0dB)。頻率f180可以用下式來計算:
其中||表示複數的絕對值(例如|a+jb|=[a+b])。而頻率f0dB有以下的關係:
增益裕度及相位裕度
增益裕度
增益裕度(gainmargin,GM)是衡量系統穩定程度的一種方法。在波德相點陣圖上可以找到βAOL相位到達-180度時的頻率,該頻率即為f180,之後就可以在增益圖上找到該頻率時βAOL的大小。
若|βAOL|180=1,表示此系統不穩定。若|βAOL|180<1,此系統穩定,而|βAOL|分貝值和0dB(對應增益大小為1)的距離表示系統距離不穩定的程度,稱為增益裕度。
增益裕度也可以用下式表示:
相位裕度
相位裕度(phasemargin,PM)是另一種衡量系統穩定程度的方法。在波德增益圖上可以找到|βAOL|大小為1的頻率,該頻率即為f0dB,之後就可以在相點陣圖上找到該頻率時βAOL的相位。
若βAOL(f0dB)的相位>−180°,表示在任何頻率時系統都會穩定,因為在f180時大小已小於1,f0dB時的相位和-180度之間的差稱為相位裕度。
若只是單純要判斷系統是否穩定,在系統為最小相位系統時,若f0dB<f180成立,則系統穩定.
若是非最小相位系統,需要用其他方式判斷穩定性,如奈奎斯特圖
優勢
 伯德圖
伯德圖但是在電子電路中,這種圖有可能比較麻煩,一方面,要表示一個網路在低頻和高頻下的所有情況,那么橫軸(頻率軸會很長)。此外,一般放大電路的放大倍數可能達到幾百,使得縱軸也很長。第三,這樣畫出的圖形往往是很不規則的曲線。
波特(Bode)圖是根據上述三點作了改進:
1.橫坐標的頻率改成指數增長,而不是以前的線性增長,比如頻率刻度為。10、100、1000、10^4、等,每一小格代表不同的頻率跨度。使一條橫軸能表示如1hz到10hz這么大的頻率範圍。一個更為有用的原因是這樣做符合人耳對聲音的敏感程度(對數效應)。
2.縱坐標表示放大倍數以10為底的對數的20倍,這是根據分貝的定義做的。這樣縱坐標的值大概0到60就足夠了。這樣在圖中一眼就能看出放大的分貝數。相頻特性也可以相應的畫。
3.把曲線做直線化處理。畫圖所依據的式子中會得到fLfH的數值。得出的伯德圖也應該在fL和fH處出現拐角(此點所在的頻率稱為截斷頻率),不過這樣處理會產生一定的誤差。理論計算可知:在截斷頻率處真實值與估計值有3dB的誤差。在斜率不為0的直線處要標明斜率。標明出每十倍頻程放大倍數的變化情況。經過這三種簡化,伯德圖的曲線就是由一條折線組成看起來非常舒服。雖然經過處理造成了誤差,但已經成為一種標準。
範例
考慮以下的低通RC電路,如下圖,其頻域的轉換函式如下:由轉換函式可以得到其截止頻率fc(以Hz為單位)為:
另一種等效表示法為:
ωc=1/(RC)
其中ωc為截止角頻率,單位是弧度每秒。
以角頻率表示的轉換函式如下:
H(jω)=(1+jω/ωc)-1
上述的方程式是一個正規化後的轉換函式,其波德圖如圖4,後續將介紹如何用直線來近似波德圖。
增益圖
上述轉換函式的增益(以分貝表示)和頻率的關係如圖5所示。
若在對數尺度的頻率下繪製不同頻率的增益,上式可以用二條直線近似,而這二條線也就是其波德圖增益圖的二條漸近線:
在角頻率小於ωc時,因ω/ωc/項較小,相對1而言可以忽略,因此其增益值為定值1,在增益圖上是一條位在0dB的水平線。
在角頻率大於ωc時,因ω/ωc項比較大,相對而言1可以忽略,因此式子簡化為-20log(ω/ωc),是斜率為-20dB/十倍頻的斜線。
上述的二條線在截止頻率ωc處交會,在圖5可以看出,當頻率遠低於截止頻率時,電路的衰減量是0dB,對應其通帶增益為1,此時濾波電路的輸出值和輸入值相同,而當頻率高於截止頻率時,信號會被電路衰減,越高頻的信號其衰減量越大。
相點陣圖
上述轉換函式的相位和頻率的關係如下
φ=-arctan(ω/ωc)
其中,ω、ωc分別是輸入角頻率及截止角頻率。當輸入角頻率遠小於截止角頻率時(ω<<ωc),比例ω/ωc的數值很小,因此相位角接近零度。當頻率增加,相位角的絕對值也隨之增加。在(ω=ωc)時為-45度。當輸入角頻率遠大於截止角頻率時(ω>>ωc,ω→∞),相位角會趨近-90度。
正規化圖
波德圖(包括幅頻圖及幅相圖)的橫軸頻率部份均可以用正規化的頻率(無因次頻率,ω<<ωc)表示。此時的圖稱為正規化的波德圖,而且其中不需考慮頻率的單位,因為頻率已改用頻率和截止頻率的比值來表示。