伊藤引理較早版本
第一引理
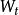 伊藤引理
伊藤引理 伊藤引理
伊藤引理設布朗運動以及二次可導函式,以下等式成立:
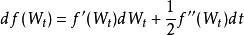 伊藤引理
伊藤引理其主要可通過對多項式環到形式冪級數的拓展,例如:
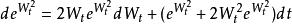 伊藤引理
伊藤引理第二引理
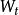 伊藤引理
伊藤引理 伊藤引理
伊藤引理設布朗運動以及二次可導函式,以下等式成立:
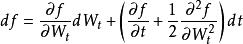 伊藤引理
伊藤引理第三引理
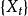 伊藤引理
伊藤引理定義伊藤過程 又稱擴散過程有以下特性:
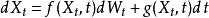 伊藤引理
伊藤引理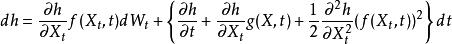 伊藤引理
伊藤引理到半鞅的拓展
連續半鞅
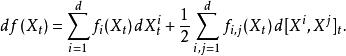 伊藤引理
伊藤引理不連續半鞅
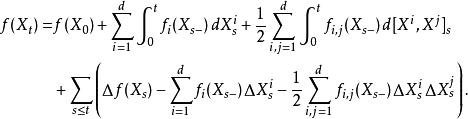 伊藤引理
伊藤引理泊松過程
我們也可以定義非連續隨機過程的函式。
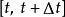 伊藤引理
伊藤引理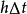 伊藤引理
伊藤引理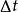 伊藤引理
伊藤引理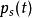 伊藤引理
伊藤引理定義跳躍強度 h,根據跳躍的泊松過程模型,在區間上出現一次跳躍的機率是加上的高階無窮小量。 h可以是常數、顯含時間的確定性函式,或者是隨機過程。在區間[0,t]上沒有跳躍的機率稱為生存機率,其變化是:
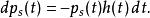 伊藤引理
伊藤引理因此生存機率為:
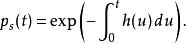 伊藤引理
伊藤引理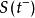 伊藤引理
伊藤引理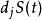 伊藤引理
伊藤引理定義非連續隨機過程S(t),並把記為從左側到達''t''時''S''的值,記是一次跳躍導致S(t)的非無窮小變化。有:
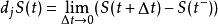 伊藤引理
伊藤引理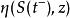 伊藤引理
伊藤引理是跳躍幅度''z''的[[機率分布]],跳躍幅度的期望值是:
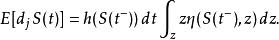 伊藤引理
伊藤引理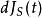 伊藤引理
伊藤引理定義補償過程和[[鞅]]:
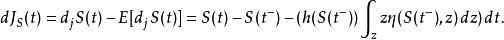 伊藤引理
伊藤引理因此跳躍的非無窮小變化,也就是隨機過程的跳躍部分可以寫為
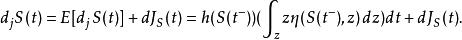 伊藤引理
伊藤引理因此如果隨機過程S同時包含漂移、擴散、跳躍三部分,可以寫為:
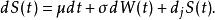 伊藤引理
伊藤引理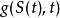 伊藤引理
伊藤引理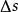 伊藤引理
伊藤引理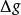 伊藤引理
伊藤引理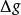 伊藤引理
伊藤引理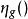 伊藤引理
伊藤引理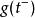 伊藤引理
伊藤引理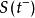 伊藤引理
伊藤引理 伊藤引理
伊藤引理考慮其函式。S(t)跳躍的幅度,會導致g(t)跳躍幅度。取決於的跳躍分布,有可能依賴於跳躍前的函式值,函式微分''dg''以及跳躍前的自變數值。的跳躍部分是:
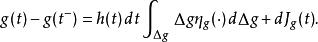 伊藤引理
伊藤引理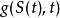 伊藤引理
伊藤引理函式的伊藤引理是:
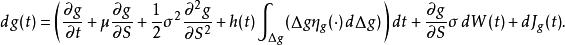 伊藤引理
伊藤引理可以看到,漂移-擴散過程與跳躍過程之和的伊藤引理,恰恰是各自部分伊藤引理的和。
套用
伊藤引理是研究隨機過程和解隨機微分方程的重要特性,在金融數學裡有廣泛的套用。例如布萊克-斯科爾斯模型
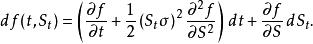 伊藤引理
伊藤引理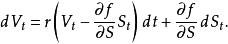 伊藤引理
伊藤引理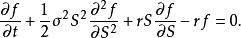 伊藤引理
伊藤引理