基本介紹
代號編碼(dummy coding)是一種簡單的編碼方法。代表不同類目的一組符號稱為“碼子”(code)。對不同類目分配碼子稱為“編碼”(coding)。在類別變數的回歸分析中，首先要對類別變數的各類目進行編碼，然後再進行回歸分析。代號編碼的方法是對給定的類目的成員分配以數字1，非該類目的成員分配以數字0，從而產生若干向量。
代號編碼
代號編碼 代號編碼 代號編碼
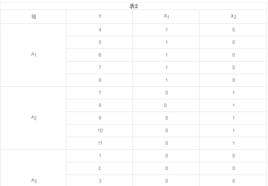
代號編碼例如，有三組被試在三種不同訓練方法下的得分如下表1所示。我們將因變數的量數合成表2中的列向量y，然後使用代號編碼方法得到列向量 與 。一般來說，類目數為k，則產生k-1個列向量。根據表2的編碼結果，就可求得y對 與 的回歸方程 。經F檢驗知，此方程具有統計上的顯著性意義 。
三種訓練方法的得分，如表：
| A | A | A |
| 4 | 7 | 1 |
| 5 | 8 | 2 |
| 6 | 9 | 3 |
| 7 | 10 | 4 |
| 8 | 11 | 5 |
三組數據的代號編碼，如表：
| 組 | Y | X | X |
| A | 4 | 1 | 0 |
| 5 | 1 | 0 | |
| 6 | 1 | 0 | |
| 7 | 1 | 0 | |
| 8 | 1 | 0 | |
| A | 7 | 0 | 1 |
| 8 | 0 | 1 | |
| 9 | 0 | 1 | |
| 10 | 0 | 1 | |
| 11 | 0 | 1 | |
| A | 1 | 0 | 0 |
| 2 | 0 | 0 | |
| 3 | 0 | 0 | |
| 4 | 0 | 0 | |
| 5 | 0 | 0 |
代號編碼的種類
在計算機軟體系統的運作中，代號編碼設計是一件非常重要的工作。通常在進行系統的輸入設計時，代號編碼的設計工作必須同時進行。一個好的編碼系統，它具有輸入者容易記憶、節省輸入數據的時間、易於調試檢查等優點。當然如果編碼方式設計得不好，那反而會成為數據管理上的一個重大缺陷。
代號編碼的種類很多，各有其編號的規則。根據一般常用的編碼方法，可以歸納為下列幾種 ：
1．順序編碼(sequence code)
順序編碼就是一般所說的流水號。流水號是最常用的方法，但通常不獨立使用。它的編碼方法基於事物發生的時間先後順序，按照時間順序的先後給予連續性的序號。
這種編碼方式簡單，但是號碼本身除了含有發生的先後順序以外，並沒有太大的意義，而且也不容易記憶，這是其主要缺點。像銀行對等候處理的交易檔案，大部分都賦予一個連續性的編號，以決定此交易檔案處理的先後順序。
2．區段編碼(block code)
區段編碼的編碼方法，是將編號對象實現按某些設定的歸類條件分段，並在各分段間保留數個可用的號碼，以利於該段內其他流水號碼的插入。
這種編碼方式的優點是可以從編碼中了解該號碼是屬於哪一部門的。郵政編碼的編碼方式就類似於此，另外有些學校的分機號碼也利用這種編碼原理，如表3所示。
| 分 類 | 分機號碼 | 分機號碼意義 |
| 7600 | 7601 | 工管系序號一號電話 |
| 7602 | 工管系序號二號電話 | |
| 7700 | 7701 | 企管系序號一號電話 |
| 7702 | 企管系序號二號電話 |
3． 分類編碼(group classification code)
分類編碼是將數據按其特性和種類分成幾大類，而每一大類可能會再細分成幾小類，然後再按對象的先後順序編上流水號來識別。
這種編碼的優點是能夠很明顯地區別對象的內容，歸類方便，而且容易識別，只是如果分類太細可能會造成位數過多。身份證號碼的編號方式、學生學號的編號方式都屬於這一類。例如，某大學學生學號的編碼方式是取九位數編碼，其中第一位代表學位別，第二至五位表示畢業的學年度，第六位代表系別，而第七至九位代表學生在該系當年度入學的流水號，如圖1所示。
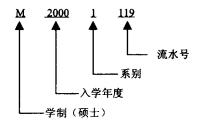圖1(a) 大學生學號的編碼方式
圖1(b) 大學生學號的編碼方式4．助記編碼(mnemonic code)
助記編碼的方法，是取對象數據某一部分的名稱、規格或種類作為編碼的組件，再將各組件予以組合成為對象的編碼。
這和編碼方式的優點是規則簡單、易記且容易編碼。例如，唯讀存儲器(read-only memory)縮寫為ROM，隨機存取記憶體(random-access memory)縮寫為RAM，各校的英文代碼也是取其英文全名的頭一個英文字母所組成，中華人民共和國(People's Republic of China)的英文縮寫是PRC等。
5．矩陣編碼(matrix code)
矩陣編碼的方法，是將對象先按其類別特性的不同予以分類，然後在各大分類下再按其相同的小分類分別給予相同的編號。這種編碼方式的優點是易於編碼、易於記憶 。
