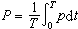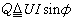交流電路中的功率
交流電路中的功率
正文
單位時間內交流電路中電場驅動電流所作的功。交流電路中的功率有多種,包括瞬時功率、有功功率、無功功率、視在功率和復功率。  交流電路中的功率瞬時功率 在正弦穩態下,線性時不變一連線埠網路(圖1)的連線埠電壓u與連線埠電流i之積稱為輸入該網路的瞬時功率,用P 表示。即
交流電路中的功率瞬時功率 在正弦穩態下,線性時不變一連線埠網路(圖1)的連線埠電壓u與連線埠電流i之積稱為輸入該網路的瞬時功率,用P 表示。即 P=ui
若將 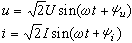
代入上式,得 
或者 
式中I、U 為i、u的平均值,ψi、ψu為初相角。  交流電路中的功率瞬時功率的波形如圖2所示(圖中設ψi=0,ψu>0)。由圖可知,瞬時功率的周期是電壓(或電流)的周期的二倍,並且在其變化的每個周期中都有在一段時間內取正值(此時電壓與電流同號,表明在這段時間內電源將能量送進一連線埠網路);在另一段時間內取負值(此時電壓與電流異號,表明在這段時間內一連線埠網路將能量送回電源)。出現這種能量在電源和網路之間往返交換的現象,是由於網路內部除了電阻元件外尚有儲能元件(電感元件和電容元件)。這些儲能元件之間不僅能相互交換能量,而且還會將所儲存的部分電磁能量送回電源。
交流電路中的功率瞬時功率的波形如圖2所示(圖中設ψi=0,ψu>0)。由圖可知,瞬時功率的周期是電壓(或電流)的周期的二倍,並且在其變化的每個周期中都有在一段時間內取正值(此時電壓與電流同號,表明在這段時間內電源將能量送進一連線埠網路);在另一段時間內取負值(此時電壓與電流異號,表明在這段時間內一連線埠網路將能量送回電源)。出現這種能量在電源和網路之間往返交換的現象,是由於網路內部除了電阻元件外尚有儲能元件(電感元件和電容元件)。這些儲能元件之間不僅能相互交換能量,而且還會將所儲存的部分電磁能量送回電源。
當ψu-ψi=0時,一連線埠網路等效於一個電阻R,則由 
上式可知,在任何時刻均有PR≥0,說明電阻始終在消耗功率,而無能量外送。
當ψu-ψi=90°時,一連線埠網路等效於一個電感L,此時 
可見PL是一個頻率為電壓(或電流)頻率的二倍、初相為2ψi的正弦函式。其值為正時,表示電感儲存能量;為負時,表示電感釋放能量。電感的這種時而儲存能量,時而又將儲存的能量如數釋放出去,說明它與外電路有能量交換。當然,上述儲存和釋放的能量是電流流過電感時儲存在磁場中的能量。
當ψu-ψi=-90°時,一連線埠網路等效於一個電容C,此時 
對Pc可作類似於PL的解釋。電容與外電路也有能量交換,它所儲存和釋放的能量是在電壓作用下儲存在電場中的能量。
有功功率 瞬時功率在一個周期內的平均值。又稱平均功率。用P 表示。即 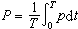
利用此式可得輸入一連線埠網路的有功功率為 
式中φ=ψu-ψi,是連線埠電壓與連線埠電流的相位差。當網路不含任何電源時,φ=ψu-ψi就是該網路的阻抗角。在工程上最感興趣的是有功功率,而不是瞬時功率,因為前者容易測量。有功功率的單位是瓦(W)。
無功功率 一種反映網路與電源之間能量反覆交換的功率。用Q表示。其定義式為 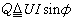
式中φ是網路的阻抗角。無功功率的絕對值是上述能量交換的最大速率,它的單位定為乏(var)。當阻抗角φ>0,網路呈感性時,由上式得Q>0,習慣上認為網路“消耗”了無功功率;當阻抗角φ<0,網路呈容性時,則得Q<0,習慣上認為網路“產生”了無功功率。無功功率雖不反映網路吸收的功率,但它的出現會導致電源與網路間的傳輸線上因電流增大而損耗增加,從而導致供電效率降低。
視在功率 連線埠電壓的有效值與連線埠電流有效值之積。又稱表觀功率。用S表示。即 S=UI
視在功率與有功功率、無功功率之間的關係為 
為了與有功功率相區別,視在功率習慣上採用伏安(VA)作單位,而不用瓦(W)。
一般電工設備的容量以視在功率標出。例如,一台交流同步發電機標稱容量為125000千伏安,指的就是由該機額定電壓與額定電流之積決定的視在功率。
復功率 連線埠電壓相量與連線埠電流相量的共軛複數之積,稱為網路吸取的復功率。用埅表示。即 
復功率並非真實的功率。定義復功率的目的是為了能用相量法求得的電壓和電流相量簡便地計算出網路的各種功率。埅與S、P、Q之間有如下的關係: 
即S是埅的模,P是埅的實部,Q是埅的虛部。
利用特勒根定理,可得 
式中妭和壝分別是連線埠電壓相量和連線埠電流相量的共軛複數;妭k和壝k分別是網路所含支路上的電壓相量和電流相量的共軛複數。此式表明,電源送入網路的復功率妭壝等於網路內各支路吸收的復功率之和,即復功率平衡。從上式又可以推得
前式表明有功功率平衡,後式表明無功功率平衡。
功率因數 網路吸收的有功功率與視在功率之比稱為該網路的功率因數。用λ表示,即 
式中的φ是網路的阻抗角,又稱功率因數角。配圖
相關連線

 交流電路中的功率
交流電路中的功率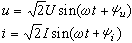


 交流電路中的功率
交流電路中的功率