基本定義
 五次函式
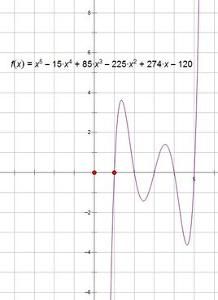
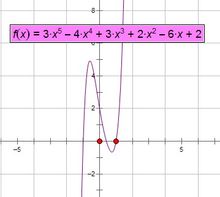
五次函式一般的,自變數x和因變數y存在如下關係:y=ax^5+bx^4+cx^3+dx^2+ex+f的函式,稱y為x的五次函
數。其中,a、b、c、d、e分別為五次、四次、三次、二次、一次項係數,f為常數,a≠0。在實際中,一般不使用此函式。
求解方法
一般的五次方程沒有統一的公式解存在。 c1c2clone於2009年寒假在山東省濰坊市市委黨校跟江西省數學會副會長陶平生先生討論五次方程是否有公式解的時候,陶平生先生否定有統一的公式解一說。陶平生先生認為:群論是解決該問題的一種很好的方法。其實,在我們的人教B版高中數學課本《選修3-4對稱與群》里,已經說明:第一,1824年:挪威的一位年輕人阿貝爾證明了:五次代數方程通用的求根公式是不存在的;第二,伽羅瓦證得了5次及其以上方程沒有統一的求根公式;第三,伽羅瓦能給出恰好有H=Sn的方程,而在群論裡面很容易證明當n≥5時,Sn不是一個可解群 。但可以用二分法近似的求出方程的解。
五次函式f(x)=ax^5+bx^4+cx^3+dx^2+ex+f其導數為f‘(x)=5ax^4+4bx^3+3cx^2+2dx+e,對於其導數,我們可以對函式進行求極值點與求其單調區間。