定義
設有兩個平穩隨機信號x(t)與y(t)，根據隨機過程理論，它們之間的統計相關特性，應該用其互相關函式表達。對x(t)與y(t)的互相關函式進行傅立葉變換，獲得其頻域中的功率密度譜，即稱為互功率密度譜，也稱互頻譜。可見，互譜與互相關函式是分別從頻域和時域描述兩個信號統計相關的兩種不同表示，它們互為傅立葉變換。互譜也適用於確定性信號分析。互譜在通信及信號處理領域中有重要用途，可用來測定一個未知參數的線性系統的頻率回響。這時主要要測出系統輸入和輸出信號之間的互譜。互譜也可以用於系統時延，如聲納接收信號等時延估計。
在實用中，通常利用快速傅立葉變換來計算和測量互譜，這是因為實際要求提高測量運算速度而提出來的，已經生產了許多測量功率譜密度函式的儀器，它們也可以用於互譜的測量。
倒譜
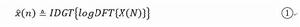圖1 公式 設離散信號序列 { x(n)，n=1,2,3，‘’‘，N-1 }，如果它的離散傅立葉變換及反變換用DFT及IDFT表示，則的倒譜定義為圖1。
圖2 若用Z變換來表示DFT，則上式定義可以改寫成圖2
式中X(Z)是x(n)的Z變換。
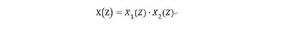圖3 倒譜在信號處理有著廣泛的用途，它主要的功能是可以線性分離經卷積後的兩個或多個分別的信號。其原理是顯而易見的。假若兩個信號分別為而x(n)及x(n），卷積後的信號為x(n)，對x(n)的Z變換X(Z)應為圖3
圖4 這樣對x(n)的倒譜圖4
利用線性濾波方法即可以將分開。這就實現到對卷積信號的信號分離。
以上處理過程所形成的系統，有如下的形式圖5
這種系統常稱為產生倒譜的同態系統。
在通信、地震信號、地質勘察信號以及語聲信號分析中，由於經常遇到這類卷積信號序列，所以倒譜分析在這些領域找到廣泛的套用。
功率譜的對數值的逆傅氏變換稱為倒譜，又稱作功率倒頻譜。廣泛套用於語音信號處理。
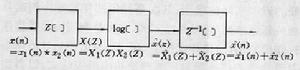圖5 倒譜的同態系統 倒頻譜函式C(q)(power cepstrum)其數學表達式為：
C(q) = | IF(log(s(f))) |^2.
其中，s(f)是信號s(t)的傅立葉變換，log（）為取對數，IF為逆傅立葉變換。
倒譜（cepstrum）就是一種信號的傅立葉變換經對數運算後再進行傅立葉反變換得到的譜。
圖6 倒譜的計算過程 計算過程如圖6：
展望
現代譜分析是20世紀70年代發展起來的新興學科。新的方法、新的軟體以及新的VLSI譜分析專用硬體不斷出現，並在越來越多的領域中獲得成功的套用。在現代譜分析理論和方法的研究中，ARMA參數模型方法和特徵分析方法是人們十分關心的研究課題。在參數模型方法中對AR方法的研究比較成熟。雖然從理論上說ARMA方法應當具有比AR方法更優越的性能，但現在還沒有有效的ARMA譜估計方法。已經提出的方法不是性能不夠理想，就是計算太複雜，距實際套用相差甚遠。現代譜估計中的特徵分析方法都有優越的譜分析性能。特徵方法和子空間理論的研究在陣列信號處理中對提高方位估計的分辨力和估計精度均有重要意義。
由於實際信號的時變、非平穩等複雜情況，研究多種信號的韌性(robust)譜估計，以及研究時變譜估計是譜分析研究的一個重要方面。對於實際套用中經常遇到的如噪聲中單個或多個正弦信號的頻率估計，窄帶信號和寬頻信號譜分析，以及淹沒在噪聲中的信號的譜分析等問題也是今後研究的重要課題。
為了加速現代譜分析方法的實際套用，人們重視快速算法和有效的算法結構的研究，尤其是能夠用超大規模積體電路硬體實現的實時譜分析方法。多維譜估計和高階譜估計的研究受到重視，其中人們十分感興趣的研究課題是對雙譜和三譜估計的研究，可用於估計信號中的相位和描述時間序列的非線性特性等。
