二體運動方程

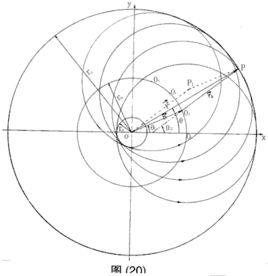
對某一個天體的運動起主導作用的力，是另一個質量更大、相距較近的天體對它的吸引力。比如在太陽系內，按照引力性質就可以劃分為行星空間和星際空間。在星際空間主要以太陽的引力為主來計算的，如人造衛星則是以地球的行星空間為主來計算的。在初步的分析中，往往把天體運動簡化並抽象為兩個質點m、M（位於天體質心）在相互引力作用下的運動，這就是二體運動

運動方程：

設M、m的向徑是R,那么他們的向徑加速度就是R關於時間t的二階導數：d^2(R)/(dt)^2（就是R對t的二階導數）根據萬有引力定律，向徑加速度應該等於向心力與質量m的比，即-uR/（r^3）以上兩則相等，於是得到二體運動方程：

d^2(R)/(dt)^2=-uR/（r^3）

（在這裡R是向量，r是R的模；u是地球引力常數，是人造地球衛星運動中常用的常數，具體的公式u=GM,G為萬有引力常數，M是地球質量。這個應該好理解，就是萬有引力公式的變形）