二項測度

二項測度（binomial measure）是一種重要的機率測度。對所有的二項測度μP滿足重分形機理。

簡介

二項測度是一種重要的機率測度。

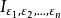二項測度

設P=(p,p)為機率向量，p>0，p>0，p+p=1。令表示[0,1]區間的n階2進區間：若ε=0，則表示取它的j-1階母區間的左半部分；若ε=1，則表示取上述區間的右半部分。設μ是[0,1]上的滿足

的惟一的機率測度。測度μ稱為二項測度。

對所有的α，μ滿足重分形機理。

重分形機理

重分形機理是重分形分析中的一個重要概念。

如果對α有dimE=f(α)=τ*(α)，則稱測度μ對於α滿足重分形機理。

重分形分析的重要目的之一是研究什麼樣的測度滿足重分形機理。

機率測度

(probability measure)

機率測度是機率論、遍歷理論等數學分支中常用的一種重要的有限測度。

在數學中，機率測度是在滿足測度屬性（如可加性）的機率空間中的一組事件上定義的實值函式。機率測度與一般的測度概念（包括像面積或體積等概念）之間的差異在於：機率測量整個機率必須為1。