歷史
 二進制
二進制現代的二進制記數系統由戈特弗里德·萊布尼茨於1679年設計,在他1703年發表的文章《論只使用符號0和1的二進制算術,兼論其用途及它賦予伏羲所使用的古老圖形的意義》(法語:Explication de l'arithmétique binaire, qui se sert des seuls caractères 0 et 1 avec des remarques sur son utilité et sur ce qu'elle donne le sens des anciennes figures chinoises de Fohy)出現。與二進制數相關的系統在一些更早的文化中也有出現,包括古埃及、古代中國和古印度。中國的《易經》尤其引起了萊布尼茨的聯想。
埃及
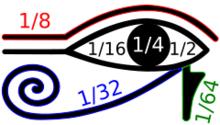
古埃及的計數員使用兩種不同的系統表示分數,一是埃及分數(與二進制記數系統無關),二是荷魯斯之眼分數(叫這個名字是因為很多數學史家相信這個系統所採用的符號可以排列成荷魯斯之眼,但這一點有爭議)。荷魯斯之眼分數是用來表示分數數量的穀物、液體等的二進制記數系統,在這一系統下,以赫卡特為單位的分數值表示成1/2、1/4、1/8、1/16、1/32和1/64等二進制分數的和。 這一系統的早期形式可以在埃及第五王朝(約公元前2400年)的檔案中找到,而發展完備的象形文字形式可追溯到埃及第十九王朝(約公元前1200年)。 古埃及做乘法的方式也與二進制數密切相關,約公元前1650年的萊因德數學紙草書中就能看到。這一計算方法中,要把1和乘數不斷翻倍,按被乘數的二進制表示從左列選出相應的2的冪次,並將右列的數相加 。
中國
 二進制
二進制《易經》的歷史可以追溯到公元前9世紀,其中的二進制記號是用來解釋其四進制占卜技術的。 它基於道的陰陽二重性。八卦和一種64卦早在古代中國的周朝就被使用了,而它們分別與三位與六位二進制數字類似。 北宋學者邵雍用一種與現代二進制數字類似的形式重新排列了卦象,不過並不是為了數學套用。在邵雍方陣中,把實線看作1、斷線看作0,從右下到左上瀏覽,那么卦象實際上就是0到63的二進制 。
印度
印度學者平甲拉(公元前兩世紀左右) 通過二進制方法來研究韻律詩。他的二進制中用到的是長短音節(一個長音節相當於兩個短音節),有些像摩爾斯電碼。與西方的位置表示法不同,平甲拉的系統中,二進制是從右往左書寫的。
萊布尼茨前的西方先驅
1605年,弗朗西斯·培根提出了一套系統,可以把26個字母化為二進制數。此外他補充道,這個思路可以用於任何事物:“只要這些事物的差異是簡單對立的,比如鈴鐺和喇叭,燈光和手電筒,以及火槍和類似武器的射擊聲”。這對二進制編碼的一般理論有重要意義。(參見培根密碼)
萊布尼茨和《易經》
 二進制
二進制萊布尼茨關於二進制的論文全名是《論只使用符號0和1的二進制算術,兼論其用途及它賦予伏羲所使用的古老圖形的意義》(1703年)。類似於現代二進制計數系統,萊布尼茲的系統使用0和1 。
後來的發展
1854年,英國數學家喬治·布爾發表了一篇里程碑式的論文,其中詳細介紹了一種代數化的邏輯系統,後人稱之為布爾代數。他提出的邏輯演算在後來的電子電路設計中起基礎性作用。
1937年,克勞德·香農在麻省理工大學完成了其電氣工程碩士學位論文,用繼電器和開關實現了布爾代數和二進制算術運算。論文題為《繼電器與開關電路的符號分析》(A Symbolic Analysis of Relay and Switching Circuits),其中香農的理論奠定了數字電路的理論基礎。香農憑這篇論文於1940年被授予美國阿爾弗雷德·諾貝爾協會美國工程師獎。哈佛大學的哈沃德·加德納稱,香農的碩士論文“可能是本世紀最重要、最著名的碩士學位論文”。
1937年11月,任職于貝爾實驗室的喬治·斯蒂比茲發明了用繼電器表示二進制的裝置。它是第一台二進制電子計算機。
進制轉換
十進數轉成二進數
整數部分,把十進制轉成二進制一直分解至商數為0。讀餘數從下讀到上,即是二進制的整數部分數字。 小數部分,則用其乘2,取其整數部分的結果,再用計算後的小數部分依此重複計算,算到小數部分全為0為止,之後讀所有計算後整數部分的數字,從上讀到下。
將59.25轉成二進制:
整數部分:
59 ÷ 2 = 29 ... 1
29 ÷ 2 = 14 ... 1
14 ÷ 2 = 7 ... 0
7 ÷ 2 = 3 ... 1
3 ÷ 2 = 1 ... 1
1 ÷ 2 = 0 ... 1
小數部分:
0.25×2=0.5
0.50×2=1.0
59.25(10)=111011.01(2)
也可以公式來計算
59.25(10) = 101*10101+1001*10100+10*1010-1+101*1010-10
= 101*1010+1001+10/1010+101/1010/1010
= 110010+1001+(10+0.1)/1010
= 111011+0.01
= 111011.01
二進數轉成十進數
將100101轉換為十進制形式如下:
•100101= [ (1) × 2] + [ (0) × 2] + [ (0) × 2] + [ (1) × 2] + [ (0) × 2 ] + [ (1) × 1 ]
•100101= [1× 32 ] + [0× 16 ] + [0× 8 ] + [1× 4 ] + [0× 2 ] + [1× 1 ]
•100101= 37
數表
| 十進制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 二進制 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
| 十進制 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 二進制 | 1011 | 1100 | 1101 | 1110 | 1111 | 10000 | 10001 | 10010 | 10011 | 10100 | 10101 |
| 十進制 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| 二進制 | 10110 | 10111 | 11000 | 11001 | 11010 | 11011 | 11100 | 11101 | 11110 | 11111 | 100000 |
二進制化為八進制
把二進制化為八進制也很容易,因為八進制以8為基數,8是2的冪(8=2),因此八進制的一位恰好需要三個二進制位來表示。八進制與二進制數之間的對應就是上面表格中十六進制的前八個數。二進制數000就是八進制數0,二進制數111就是八進制數7,以此類推。
| 八進制 | 二進制 |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
八進制轉為二進制:
•65= 110 101
•17= 001 111
二進制轉八進制:
•101100= 101 100(三位一組) = 54
•10011= 010 011(用零填充 (密碼學),三位一組) = 23
八進制轉十進制:
•65= (6 × 8) + (5 × 8) = (6 × 8) + (5 × 1) = 53
•127= (1 × 8) + (2 × 8) + (7 × 8) = (1 × 64) + (2 × 8) + (7 × 1) = 87
套用
二進制的套用非常廣泛,可以套用於各個方面,比如計算機科學,物理學等 。
二進制的集合運算
已知集合A,求A的冪集 。
由於集合子集中的元素與子集下標中二進制位的“l”相對應,因此求子集中元素的運算可以轉化為尋找子集下標二進制位中“l”所在位置的運算,此運算可以利用移位操作來實現。
例如,求101所對應的A的子集,我們可以通過3次移位,每次先將當前的數值與數值1相與,如果結果等於1,則本次第0位上的值為l,否則為0,由移位的次數可以知道當前第0位的l在原數據中的位置,從而找到對應的實際元素。運算如下:
①第0次與:lOl&001=1,a對應二進制位的第0位,而且本次相與的結果為1,所以a屬於此子集:101右移一位,現在的數值為010
②第1次與:010&001=0,b對應二進制位的第l位,而且本次相與的結果為0,所以b不屬於此子集。OlO右移一位,現在的數值為001③第1次與:001&001=l,C對應二進制位的第2位,而且本次相與的結果為1,所以C屬F此子集。001右移一位,現在的數值為000。
計算完畢。求出101對應的A的子集為{a,c}。

