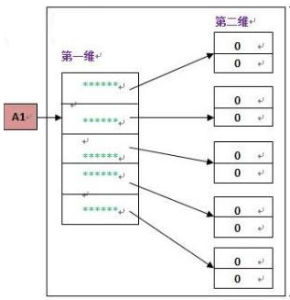
概述
二維數組A[m][n],每個元素的長度為t個位元組,設a[p][q]為A的第一個元素,即二維數組的行下標從p到m,列下標從q到n,按“行優先順序”存儲時則元素a[i][j]的地址計算為:
LOC(a[i][j]) = LOC(a[p][q]) + ((i − p) * n + (j − q)) * t
按“列優先順序”存儲時,地址計算為:
LOC(a[i][j]) = LOC(a[p][q]) + ((j − q) * m + (i − p)) * t
存放該數組至少需要的單元數為(m-p+1) * (n-q+1) * t 個位元組
二維數組又稱為矩陣,行列數相等的矩陣稱變方陣。對稱矩陣a[i][j] = a[j][i],對角矩陣:n階方陣的所有非零元素都集中在主對角線上.
二維數組基本運算算法
:
(1)轉置矩陣://其中A, B是m*n矩陣:
void tramat(matrix A,matrix B){ int i,j;
for(i=0; i<m; i++)
for(j=0;j<n;j++)
B[j]=A[j];
}
(2)矩陣相加://其中A,B,C是m*n矩陣:
void addmat(matrix C, matrix A, matrix B){
int i, j;
for(i=0; i<m; i++)
for(j=0;j<n;j++)
c[j] = A[j] + B[j];
}
(3)矩陣相乘://其中A是m*n矩陣,B是n*1矩陣,C為m*1矩陣
void mutmat(matrix C, matrix A, matrix B){
int i, j, k;
for(i=0; i<m; i++)
for(j=0; j<i; j++){
C[j]=0;
for(k=0; k<n; k++)
C[j] = C[j] + A[k] * B[k][j];
}
}