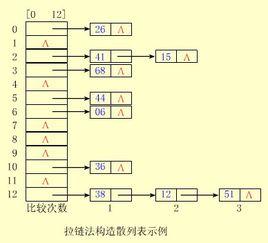
散列表
設所有可能出現的關鍵字集合記為U(簡稱全集)。實際發生(即實際存儲)的關鍵字集合記為K（|K|比|U|小得多）。
散列方法是使用函式h將U映射到表T[0..m-1]的下標上（m=O(|U|)）。這樣以U中關鍵字為自變數，以h為函式的運算結果就是相應結點的存儲地址。從而達到在O(1)時間內就可完成查找。
其中：
① h：U→{0，1，2，…，m-1} ，通常稱h為散列函式(Hash Function)。散列函式h的作用是壓縮待處理的下標範圍，使待處理的|U|個值減少到m個值，從而降低空間開銷。
② T為散列表(Hash Table)。
③ h(Ki)(Ki∈U)是關鍵字為Ki結點存儲地址(亦稱散列值或散列地址)。
④ 將結點按其關鍵字的散列地址存儲到散列表中的過程稱為散列(Hashing)
衝突
兩個不同的關鍵字，由於散列函式值相同，因而被映射到同一表位置上。該現象稱為衝突(Collision)或碰撞。發生衝突的兩個關鍵字稱為該散列函式的同義詞(Synonym)。
安全避免衝突的條件
最理想的解決衝突的方法是安全避免衝突。要做到這一點必須滿足兩個條件：
①其一是|U|≤m
②其二是選擇合適的散列函式。
這隻適用於|U|較小，且關鍵字均事先已知的情況，此時經過精心設計散列函式h有可能完全避免衝突。
衝突不可能完全避免
通常情況下，h是一個壓縮映像。雖然|K|≤m，但|U|>m，故無論怎樣設計h，也不可能完全避免衝突。因此，只能在設計h時儘可能使衝突最少。同時還需要確定解決衝突的方法，使發生衝突的同義詞能夠存儲到表中。
影響衝突的因素
衝突的頻繁程度除了與h相關外，還與表的填滿程度相關。
設m和n分別表示表長和表中填人的結點數，則將α=n/m定義為散列表的裝填因子(Load Factor)。α越大，表越滿，衝突的機會也越大。通常取α≤1。對於大多數應用程式來說，裝填因子為0.75是比較合理的。
標準
散列函式的選擇有兩條標準：簡單和均勻。
簡單指散列函式的計算簡單快速；
均勻指對於關鍵字集合中的任一關鍵字，散列函式能以等機率將其映射到表空間的任何一個位置上。也就是說，散列函式能將子集K隨機均勻地分布在表的地址集{0，1，…，m-1}上，以使衝突最小化。
常用散列函式
平方取中法
具體方法：先通過求關鍵字的平方值擴大相近數的差別，然後根據表長度取中間的幾位數作為散列函式值。又因為一個乘積的中間幾位數和乘數的每一位都相關，所以由此產生的散列地址較為均勻。
例：將一組關鍵字(0100，0110，1010，1001，0111)平方後得
(0010000，0012100，1020100，1002001，0012321)
若取表長為1000，則可取中間的三位數作為散列地址集：
(100，121，201，020，123)。
相應的散列函式用C實現很簡單：
int Hash(int key){ //假設key是4位整數
key*=key； key/=100； //先求平方值，後去掉末尾的兩位數
return key%1000； //取中間三位數作為散列地址返回
除余法
該方法是最為簡單常用的一種方法。它是以表長m來除關鍵字，取其餘數作為散列地址，即 h(key)=key%m
該方法的關鍵是選取m。選取的m應使得散列函式值儘可能與關鍵字的各位相關。m最好為素數。
若選m是關鍵字的基數的冪次，則就等於是選擇關鍵字的最後若干位數字作為地址，而與高位無關。於是高位不同而低位相同的關鍵字均互為同義詞。
若關鍵字是十進制整數，其基為10，則當m=100時，159，259，359，…，等均互為同義詞。
相乘取整法
該方法包括兩個步驟：首先用關鍵字key乘上某個常數A(0<A<1)，並抽取出key.A的小數部分；然後用m乘以該小數後取整。即：
該方法最大的優點是選取m不再像除余法那樣關鍵。比如，完全可選擇它是2的整數次冪。雖然該方法對任何A的值都適用，但對某些值效果會更好。Knuth建議選取
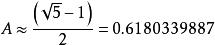二次再散列法該函式的C代碼為：
int Hash(int key){
double d=key *A； //不妨設A和m已有定義
return (int)(m*(d-(int)d))；//(int)表示強制轉換後面的表達式為整數
}
隨機數法
選擇一個隨機函式，取關鍵字的隨機函式值為它的散列地址，即
h(key)=random(key)
其中random為偽隨機函式，但要保證函式值是在0到m-1之間。
二次再散列法
開放地址法
開放地址法 解決衝突的方法
用開放地址法解決衝突的做法是：當衝突發生時，使用某種探查(亦稱探測)技術在散列表中形成一個探查(測)序列。沿此序列逐個單元地查找，直到找到給定的關鍵字，或者碰到一個開放的地址(即該地址單元為空)為止（若要插入，在探查到開放的地址，則可將待插入的新結點存人該地址單元）。查找時探查到開放的地址則表明表中無待查的關鍵字，即查找失敗。
開放地址法的一般形式
開放地址法的一般形式為： hi=(h(key)+di)%m 1≤i≤m-1
其中：
①h(key)為散列函式，di為增量序列，m為表長。
②h(key)是初始的探查位置，後續的探查位置依次是hl，h2，…，hm-1，即h(key)，hl，h2，…，hm-1形成了一個探查序列。
③若令開放地址一般形式的i從0開始，並令d0=0，則h0=h(key)，則有：
hi=(h(key)+di)%m 0≤i≤m-1
探查序列可簡記為hi(0≤i≤m-1)。
開放地址法堆裝填因子的要求
開放地址法要求散列表的裝填因子α≤l，實用中取α為0.5到0.9之間的某個值為宜。
形成探測序列的方法
按照形成探查序列的方法不同，可將開放地址法區分為線性探查法、二次探查法、雙重散列法等。
① 線性探查法(Linear Probing)
該方法的基本思想是：
將散列表T[0..m-1]看成是一個循環向量，若初始探查的地址為d(即h(key)=d)，則最長的探查序列為：
d，d+l，d+2，…，m-1，0，1，…，d-1
即:探查時從地址d開始，首先探查T[d]，然後依次探查T[d+1]，…，直到T[m-1]，此後又循環到T[0]，T[1]，…，直到探查到T[d-1]為止。
探查過程終止於三種情況：
(1)若當前探查的單元為空，則表示查找失敗（若是插入則將key寫入其中）；
(2)若當前探查的單元中含有key，則查找成功，但對於插入意味著失敗；
(3)若探查到T[d-1]時仍未發現空單元也未找到key，則無論是查找還是插入均意味著失敗(此時表滿)。
利用開放地址法的一般形式，線性探查法的探查序列為：
hi=(h(key)+i)%m 0≤i≤m-1 //即di=i
② 二次探查法(Quadratic Probing)
二次探查法的探查序列是：
hi=(h(key)+i*i)%m 0≤i≤m-1 //即di=i2
即探查序列為d=h(key)，d+12，d+22，…，等。
該方法的缺陷是不易探查到整個散列空間。
③ 雙重散列法(Double Hashing)
該方法是開放地址法中最好的方法之一，它的探查序列是：
hi=(h(key)+i*h1(key))%m 0≤i≤m-1 //即di=i*h1(key)
即探查序列為：
d=h(key)，(d+h1(key))%m，(d+2h1(key))%m，…，等。
該方法使用了兩個散列函式h(key)和h1(key)，故也稱為雙散列函式探查法。
拉鏈法
拉鏈法解決衝突的方法
拉鏈法解決衝突的做法是：將所有關鍵字為同義詞的結點連結在同一個單鍊表中。若選定的散列表長度為m，則可將散列表定義為一個由m個頭指針組成的指針數組T[0..m-1]。凡是散列地址為i的結點，均插入到以T[i]為頭指針的單鍊表中。T中各分量的初值均應為空指針。在拉鏈法中，裝填因子α可以大於1，但一般均取α≤1。
拉鏈法的優點
拉鏈法有如下幾個優點：
(1) 拉鏈法處理衝突簡單，且無堆積現象，即非同義詞決不會發生衝突，因此平均查找長度較短；
(2)由於拉鏈法中各鍊表上的結點空間是動態申請的，故它更適合於造表前無法確定表長的情況；
(3)開放定址法為減少衝突，要求裝填因子α較小，故當結點規模較大時會浪費很多空間。而拉鏈法中可取α≥1，且結點較大時，拉鏈法中增加的指針域可忽略不計，因此節省空間；
(4)在用拉鏈法構造的散列表中，刪除結點的操作易於實現。只要簡單地刪去鍊表上相應的結點即可。而對開放地址法構造的散列表，刪除結點不能簡單地將被刪結點的空間置為空，否則將截斷在它之後填人散列表的同義詞結點的查找路徑。這是因為各種開放地址法中，空地址單元(即開放地址)都是查找失敗的條件。因此在用開放地址法處理衝突的散列表上執行刪除操作，只能在被刪結點上做刪除標記，而不能真正刪除結點。
拉鏈法的缺點
拉鏈法的缺點是：指針需要額外的空間，故當結點規模較小時，開放定址法較為節省空間，而若將節省的指針空間用來擴大散列表的規模，可使裝填因子變小，這又減少了開放定址法中的衝突，從而提高平均查找速度。
多哈希法
設計二種甚至多種哈希函式，可以避免衝突，但是衝突幾率還是有的，函式設計的越好或越多都可以將幾率降到最低（除非人品太差，否則幾乎不可能衝突）。
建域法
假設哈希函式的值域為[0,m-1]，則設向量HashTable[0..m-1]為基本表，另外設立存儲空間向量OverTable[0..v]用以存儲發生衝突的記錄。
