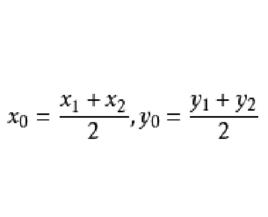基本介紹
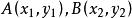 中點公式
中點公式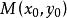 中點公式
中點公式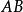 中點公式
中點公式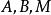 中點公式
中點公式 中點公式
中點公式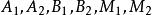 中點公式
中點公式設 是平面直角坐標系內的任意兩點,點 是線段 的中點。過點 分別向 軸作垂線,垂足分別為 ,如圖1所示。
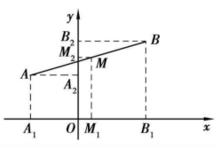 圖1
圖1 中點公式
中點公式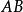 中點公式
中點公式 中點公式
中點公式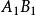 中點公式
中點公式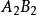 中點公式
中點公式因為點 為線段 的中點,根據平行線的性質,點 分別是線段 和 的中點,即
 中點公式
中點公式 中點公式
中點公式所以 ,即
 中點公式
中點公式這就是線段中點坐標的計算公式,簡稱 中點公式。同樣也可以將中點公式推廣到三維的情況 。
套用舉例
求連線下列兩點的線段的中點坐標。
 中點公式
中點公式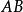 中點公式
中點公式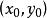 中點公式
中點公式解: (1)設線段的中點坐標為,則根據中點坐標公式可得
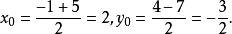 中點公式
中點公式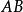 中點公式
中點公式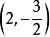 中點公式
中點公式所以線段的中點坐標為。
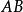 中點公式
中點公式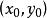 中點公式
中點公式(2) 設線段的中點坐標為,則根據中點坐標公式可得
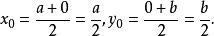 中點公式
中點公式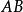 中點公式
中點公式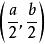 中點公式
中點公式所以線段的中點坐標為。
相關知識
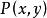 中點公式
中點公式點在平面直角坐標系中的表示: ;
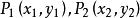 中點公式
中點公式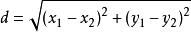 中點公式
中點公式兩點 之間的距離: 。
中心對稱:關於點的對稱問題
點關於點的對稱
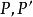 中點公式
中點公式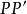 中點公式
中點公式如果點 關於點M對稱,則M是線段 的中點。
解析:依據中點坐標公式:
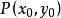 中點公式
中點公式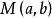 中點公式
中點公式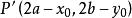 中點公式
中點公式【 】→(關於點 的對稱點)→【 】
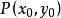 中點公式
中點公式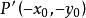 中點公式
中點公式【 】→(關於坐標原點的對稱點)→ 【 】
曲線關於點的對稱
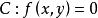 中點公式
中點公式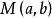 中點公式
中點公式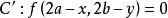 中點公式
中點公式【】→(關於點的對稱曲線)→【】
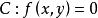 中點公式
中點公式 中點公式
中點公式【】→(關於坐標原點的對稱曲線)→ 【】
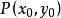 中點公式
中點公式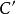 中點公式
中點公式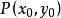 中點公式
中點公式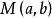 中點公式
中點公式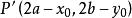 中點公式
中點公式 中點公式
中點公式 中點公式
中點公式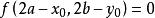 中點公式
中點公式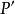 中點公式
中點公式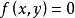 中點公式
中點公式解析:設是曲線上的任意一點,關於的對稱點為,因為在曲線上,所以,,即的坐標是方程的解 。
軸對稱問題:關於直線的對稱問題
 中點公式
中點公式點P關於直線 的對稱點
 中點公式
中點公式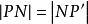 中點公式
中點公式 中點公式
中點公式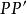 中點公式
中點公式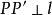 中點公式
中點公式 中點公式
中點公式過點P做的垂線,垂足為N,延長PN到P’,使,則是線段的中點,,N在直線上。
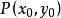 中點公式
中點公式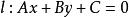 中點公式
中點公式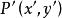 中點公式
中點公式設關於直線的對稱點為,則有
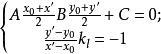 中點公式
中點公式 中點公式
中點公式 中點公式
中點公式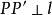 中點公式
中點公式其中第一個方程式是因為在直線上),第二個方程式是因為。
解得:
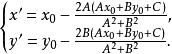 中點公式
中點公式 中點公式
中點公式曲線關於直線 的對稱
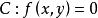 中點公式
中點公式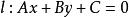 中點公式
中點公式 中點公式
中點公式曲線關於直線的對稱曲線的方程解題步驟:
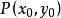 中點公式
中點公式 中點公式
中點公式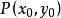 中點公式
中點公式 中點公式
中點公式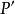 中點公式
中點公式①設是曲線上任意一點,求點關於直線的對稱點的坐標。
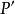 中點公式
中點公式 中點公式
中點公式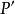 中點公式
中點公式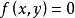 中點公式
中點公式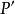 中點公式
中點公式 中點公式
中點公式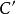 中點公式
中點公式②因為在曲線上,則的坐標方程是的解,將的坐標代入曲線的方程,化簡即得的方程 。