並行算法

並行算法就是用多台處理機聯合求解問題的方法和步驟,其執行過程是將給定的問題首先分解成若干個儘量相互獨立的子問題,然後使用多台計算機同時求解它,從而最終求得原問題的解。

並行算法

正文

適用於並行計算機的數值算法。計算機傳統結構的顯著特徵是單指令流單數據流，即每一時刻按一條指令處理一個數據。通常的數值算法適於此類計算機，可稱串列算法。20世紀60年代開始發展含大量處理機的並行計算機，它分單指令流多數據流與多指令流多數據流兩類，每一時刻分別按一條或多條指令處理多個數據。並行計算機的出現促使了適應其並行這個特點的並行算法的發展。
並行算法依賴一個簡單事實：獨立的計算可同時執行。所謂獨立計算是指其每個結果元只出現一次的計算。例如A8=α1·α2……α8中7個乘法不能同時執行,但可分成三個獨立計算組：
第一組
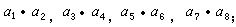
第二組
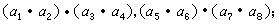
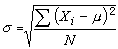
　 第三組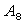。如每組的運算並行執行，計算 A8，只須三步（乘法），其步驟可用圖中的雙杈計算樹來表示。推廣此例，得到由滿足結合律的任一運算“。” 形成的表達式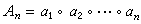的最優並行算法，稱為結合扇入算法。此算法提供了建立並行算法的一種普遍原則：反覆將每一計算分裂成具有同等複雜性的兩個獨立部份，稱為遞推倍增法。
研究表明，大量數值問題可獲得有效的並行算法。一個算法是否有效主要看加速

及所需的處理機個數 P的大小。並行算法的複雜性正是通過參數Tp、S和P來描述的。向量運算具有內在並行性（包含大量獨立計算），因而首先是在數值線代數方面，並行算法特別富有成果。
串列算法與並行算法存在固有差別。有效串列算法一般不能直接變換為並行算法，而且兩者在數值性態方面（例如數值穩定性及疊代算法的收斂速度）可以彼此大不相同。

配圖

相關連線