埃舍爾作品
一條瀑布從高處傾瀉而下,轉動著水輪。然後,水流順著磚砌的水渠向前流動。可是,這水流竟流到了瀑布上方,然後再次傾瀉而下,轉動著水輪。如此周而復始,簡直是一架永動機!而當你定睛細看時,就會發現,這水流實際上是在一個平面上流動(《瀑布》)。
在一個兩層的觀景樓里,一個豎得筆直的梯子,它的最上端斜靠在觀景樓的外邊。而梯肢卻站在樓內。不論誰爬在梯子上,都弄不清自己到底是在亭樓的裡邊還是外邊(《觀景樓》)。
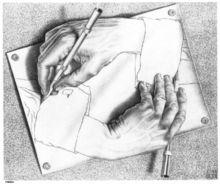
一隻手在畫另一隻手,同時,被畫的那隻手又忙著畫第一隻手,而所有這一切又都畫在一張被圖釘固定在畫板上的紙面上(《畫手》)。
…………
所有這些不可能的景象,都在荷蘭著名繪畫大師埃舍爾的筆下實現了。
 觀景樓
觀景樓埃舍爾,這位荷蘭版畫大師是獨一無二的,看他的畫是一樁奇妙的遊戲。你的第一印象會是非常精緻,具有極強的裝飾美感。然後,這些畫開始向你的智力、向你的正常思維邏輯發出挑釁,空間開始錯雜,上下、左右、內外通通顛倒,你的大腦開始暈眩……
但是,這些畫卻不是隨意的藝術幻想,而是現代數學之美在藝術上的具體體現。難怪藝術界一開始並不認可埃舍爾,他最先是在科學界獲得喝彩。諾貝爾物理學獎得主揚振寧用他的畫作《騎士》作自己所著《基本粒子發現簡史》的封面,他曾被邀請在劍橋大學國際結晶學聯合會上做演講和作品展示……
我們經常聽一些科學家說,事物的數學性中蘊含著濃郁的詩意。然而,這並不是任何人都能體會到的。面對一個公式或者理論,訓練有素的數學家和物理學家常常發出“美”的感嘆,而對於不諳此道的普通人來說,卻不過是一組無意義的符號而已。但是埃舍爾這位獨特的藝術家卻畢生在不自覺地從事著一種“翻譯”工作——把艱深的數學翻譯成一目了然、具有美感的藝術,使一般人不僅能直觀地領悟到諸如拓撲、黎曼曲面、無限這樣一些抽象的數學概念,甚至還能在心中激起愉悅感。
不可能三桿
 畫手
畫手據說埃舍爾創作《瀑布》的靈感來自英國理論物理學家、《皇帝的新腦》一書的作者彭羅斯構想的“不可能三桿”。彭羅斯把它叫做三維直角結構:三個直角都很正常,但它們是以錯誤的、在現實中根本不可能的方式連線起來的,於是就形成了這樣一個三角形,三個角之和為270度,——當然它肯定不是任何實際存在的空間結構的投射。
埃舍爾把三個這樣的“不可能三桿”連線起來,從圖中看到,我們沿著從A點走到B點是平坦,從B點到C點似乎也是平坦的,但從 C點回到A點在視覺上我們卻兀地掉了下來,這正是埃舍爾在《瀑布》中所達到的效果,而這一切只是因為構成圖形的每一個三桿都是不可能存在的。
 不可能三角形
不可能三角形埃舍爾創作了大量此類的視覺幻象作品,這一切構成了他的“不可能世界”。底下這幅石版畫《觀景樓》也很有名。稍加注意你就會發現,這個亭子建得很怪異。亭子的上層與下層居然互成直角!此外,把兩層樓台連線起來的八根柱子也很奇怪。只有最右邊和最左邊的柱子是正常的,其餘六根都是把前面連到後面,所以有些柱子肯定是會從中央的空間斜穿而過。這就造成了另一個更加荒謬的圖景:那個豎得筆直的梯子,它的最上端斜靠在觀景樓的外邊,而梯腳卻站在樓內。如果我們把畫面從中間沿水平線剪開,就會發現兩個部分都很正常。那么不言而喻,視覺上的悖謬來處於兩個部分的錯誤的連線,即上面已經提到的六根柱子的不可能的連線。
拓撲學
 莫比烏斯帶Ⅰ
莫比烏斯帶Ⅰ埃舍爾對拓撲學上有名的莫比烏斯帶很感興趣,以它創作了許多作品。我們知道,莫比烏斯帶有兩個重要的拓撲學特性,一是沿其中線剪開,它不會分成兩個環,仍然是一個;二是它只有一個面和一條邊。為了驗證前一點,你只要拿起剪刀來試一試就知道了。至於後一點,你可以從帶子的任意一處開始給它塗色,不斷地塗上顏色,而中間不會有間斷。因為假如有兩個面,塗完一個,你中間勢必要翻轉一下,才能去塗另一個面。同樣道理,你假如把手指放在邊上的任意一點,然後沿著邊不斷滑去,你的手指終究要回到起點,這就是說,它只有一條邊,並且是封閉的。
埃舍爾的《莫比烏斯帶Ⅰ》闡明了它的第一個拓撲學特性。在這幅作品中,每條蛇都咬著另一條蛇的尾巴。整個圖案就是縱向剪下的莫比烏斯帶。如果順著蛇的方向看,它們似乎始終是編在一起的;但如果我們將帶子拉開一點,就會得到帶有兩個紐結的一個完整的帶子。
 莫比烏斯帶Ⅱ
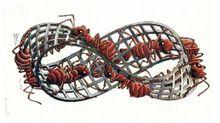
莫比烏斯帶Ⅱ木口木刻《莫比烏斯帶Ⅱ》則闡明了後一個拓撲學特性。圖中這些可憐的螞蟻沿著莫比烏斯帶做成的梯子不斷爬行,一忽兒里,一忽兒外,似乎永遠爬不到盡頭。而且假如它有知覺,一定越爬越奇怪:明明在裡頭的,怎么又莫名其妙翻上來了?這也難怪,因為這架“梯子”只有一個面,並且是完全封閉的;在這兒,里和外其實壓根兒不存在。
《畫廊》
 畫廊
畫廊石版畫《畫廊》被認為是埃舍爾一生的巔峰之餘。埃舍爾本人也認為,在這兒他已經達到了他的思維能力和表現能力的極限。在畫面的右下角,我們看到畫廊的入口,一場畫展正在進行。向左,我們遇到一位年輕人,正站在那兒看牆上的一幅畫。在這幅畫中,他看見一艘船,再往上,也就是整個畫面的左上角,是碼頭沿岸的一些房子。現在我們向右移,這排房子繼續延伸,延伸到畫面最右側,然後隨著我們的視線下移,就會發現角落裡有一座房子,房子底部有一個不足為訓的入口,畫廊里正在被認為是埃舍一場畫展……至此我們才恍然大悟,我們的這位年輕人其實正站在他觀看的那幅作品之中!這一切讓人不禁想起卞之琳的一首詩:
你在橋上看風景
看風景的人在樓上看你
明月裝飾了你的窗子
你裝飾了別人的夢
平面鑲砌
用平面鑲砌是埃舍爾一生珍愛的主題,也是他的重要技巧,貫穿於他的許多作品中。到了晚年,他還引以為豪地說:“這是我挖掘出來的最豐富的靈感之源,它至今也沒有枯竭。”
所謂平面鑲砌,就是用一組圖案對平面進行周期性地填充,這些圖案可以是簡單的,也可以是複雜的。比如把一個平面劃分成一系列等大的正方形,這也算是一種平面鑲砌,只是太簡單了。埃舍爾的圖案要複雜得多。比方他愛用人像、鳥、魚、蜥蜴來作為填充的圖案。正因為複雜,填充起來就需要很高的技巧,這中間還得嚴格遵循連續、對稱、變換、循環等數學上的基本規則。不過在埃舍爾那裡,這一切不僅做得天衣無縫,而且充滿美德。
早期,埃舍爾的周期性平面鑲砌用的是完全相同的圖形,到了晚年,他開始採用相似圖形。這是一些形狀相同,只是大小比例不等的圖形。埃舍爾試圖通過這樣的連續變形,來探討數學上另一個重要概念——“無限”。
 圓形極限Ⅲ
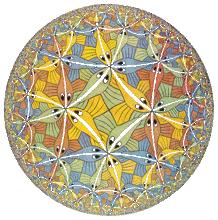
圓形極限Ⅲ《圓形極限Ⅲ》是此類作品中最具有典型的一幅。要領會這幅作品的妙處,你得想像自己是圖中的一條魚——假如你嫌這些魚不夠漂亮,那把自己想像得漂亮一點就可以了。當你沿著空白色的曲線游向圖的邊緣,你似乎跟邊緣離得更近了,但事實上在這同時你也在按著一定的比例在縮小,因此離邊緣依然一樣的遠。這個過程無限地進行下去,你只會變得無限的小,無限地接近邊界,但永遠達不到邊界,除非你有“無限”的耐心。而在邊界的圓周上,則達到了兩個極限——個體無限的小和數量上無限的多。
這幅畫不禁讓人想起數學上“有限又無限”的思想。作為一個整體,圓周所包含的區域顯然是有限的,但從圖中魚的觀點,我拚命地游,卻永遠突破不了這個魔圈,那分明又是無界。愛好科學的人們經常問:“宇宙是有限的還是無限的?”、“為什麼微觀、巨觀、宇宙觀的世界包含著那么多的相似性?”通過埃舍爾的這幅作品,他們對這些問題或許會得到更好的理解。
繪畫乃騙術
在欣賞了作品之後,少不了要探討藝術家創作的動機。那么埃舍爾創作這些“不可能世界”的動機何在?當然,好玩是一方面。不過,埃舍爾不僅是位藝術家,還是個藝術家裡的思想者。這些“好玩”的繪畫事實上包含了他對繪畫本質的更深刻的思考。他很早就意識到所有繪畫所先天具有的矛盾——那就是三維的空間必須表現在二維的平面上。因為這個內在的矛盾,他認為任何繪畫都是一種自欺欺人的騙術。既然如此,就可以通過對傳統透視法進行革新,在平面上營造出甚至在三維空間中不可能存在的世界,把觀者騙得理甚。
為了表達自己“繪畫是騙術”的觀點,埃舍爾不異“以子之矛攻子之盾”,以幻象來揭穿幻象。在著名的石版畫《畫手》中,畫面上一隻手在畫另一隻手,同時,被畫的那隻手又忙著畫第一隻手,而所有這一切又都畫在一張被固定在畫板上的紙面上。手從紙面躍然而出,你幾乎都想去抓握它,可是周圍環境的有意布置卻明白無誤地告訴你:這一切只不過是二維的平面畫。在你失望氣憤之時,畫家卻在暗處狡黠頑皮地笑了,仿佛在說:“你現在明白怎么回事了吧?”而你一旦意識到自己受了欺騙,也會跟著笑起來。
 相對性
相對性埃舍爾雖然是一個革新者,但他也創作了大量嚴格遵循傳統透視法的作品。不過即使在那些作品裡,埃舍爾也並非按部就班,而是做了大膽的創新。傳統透視法有一個規則:從我們眼前向後退的平等線要畫成通過一個稱為滅點的線束。一般一幅畫只有一個滅點,比方說一幅畫正掛著時我們看起來舒服,斜掛或者倒掛時我們一眼就看出來掛得不對頭,就是這個緣故。但在埃舍爾的某些作品裡,他用了好幾個滅點,這樣正看是對的,倒著看是對的,斜著看也還是對的。
石版畫《相對性》就屬於此類作品。這幅畫中出現三個滅點,其中的十六個小人可以分成三組,每組小人都生活在自己的世界中。而且對於所選定的任何一組小人,他們的世界都是這幅作品所畫的全部內容;只是其中一組的天花板,可能是另一組的牆;一組認為是門的東西,另一組可能認為是地板上的活動門而已。
對於這幅作品的深入研究也許會對太空人有所幫助。它將幫助太空人認識到,空間中的每一個平面都可以隨意地成為地面。他們必須習慣於看到同事隨時隨地都可能從誇張的位置出現而不會感到頭暈和困惑。
數學思想
從以上的介紹中我們大致了解了埃舍爾作品的風格。繪畫與數學思想密切相關,這既是埃舍爾有別於其他藝術家的特點,也是他的作品魅力之所在。埃舍爾所思考的問題以及創作的方式,更接近於科學家而非藝術家,所以毫不奇怪,他的作品首先為科學家們所接受,尤其是數學家把他當作“失散多年的兄弟”。
埃舍爾在自己的創作筆記中曾經寫道:“數學家打開了一扇通向無限可能性的大門,但是他們自身並沒有進入其中看看,他們特殊的稟賦使他們對如何打開這扇門的方式更感興趣。”
確實,在數學家那裡,所有的不可能都會被粉碎,空間的維度不僅是三維的,而是更多維的——現代物理學已經證明,我們所處的宇宙也許就存在更高維的空間;空間的形狀不僅是歐式幾何的,還有更多其他獨特形狀。確實,宇宙學家逐漸發現,我們宇宙的形狀可能就是拓撲結構的;無限大和無限小最終融為一體,空間有限,但沒有邊界。也許,當我們仰望夜空,在最遙遠的星球之外的某個地方,空間到了盡頭,出現了一個一無所有的邊界。
從這個意義上,我們怎么能說埃舍爾筆下的世界是不可能的呢?
作為藝術家的埃舍爾正是以自己的高超技藝展示了數學花園裡的一朵朵奇葩,不僅填補了專業數學家的缺憾,而且開創了一個獨具魅力的藝術世界。

