概述
測量天體之間的距離可不是一件容易的事。 天文學家把需要測量的天體按遠近不同分成好幾個等級。離我們比較近的天體,它們離我們最遠不超過100光年(1光年=9.461012千米)
我們平時只通過肉眼觀察,就可以知道物體的遠近,就是利用三角視差法,兩個眼睛就是兩個視點,如果閉上一隻眼睛,就不能準確判斷距離了。如果物體太遠,頂角就會變得很小,這時,就不能準確距離了,例如我們看太陽和月亮幾乎是一樣遠的。這時,可以增加兩個視點之間的距離,例如分別在北京和海口同時觀測,就可以測定比較遠的距離,用這種方法,就可以測定太陽系內的天體和附近恆星了。如果再遠些,就可以利用地球軌道直徑當底邊,先觀測一次,半年後再觀測一次。就可以測定銀河系內天體和本星系團中大多數星系了。如果再遠些,就要進一步擴大底邊,例如在天王星上設定一個望遠鏡,但我們目前不能把望遠鏡發射到那么遠的地方,於是,三角視察法就不能用了,所以,更遠的天體距離是利用哈勃定律來測定的,不過,由於哈勃常數的測定還不準確,所以,大尺度天體距離的測定也是一個估計值。
計算
河內天體的距離又稱為視差,恆星對日地平均距離(a)的張角叫做恆星的三角視差(p),則較近的恆星的距離D可表示為:sinπ=a/D
若π很小,π以角秒表示,且單位取秒差距(pc),則有:D=1/π
用周年視差法測定恆星距離,有一定的局限性,因為恆星離我們愈遠,π就愈小,實際觀測中很難測定。三角視差是一切天體距離測量的基礎,至今用這種方法測量了約10,000多顆恆星。
天文學上的距離單位除天文單位(AU)、秒差距(pc)外,還有光年(ly),即光在真空中一年所走過的距離,相當94605億千米。三種距離單位的關係是:
1秒差距(pc)=206265天文單位(AU)=3.26光年=3.09×1013千米
1光年(1y)=0.307秒差距(pc)=63240天文單位(Au)=0.95×1013千米。
測恆星距離
 三角視差法測恆星距離
三角視差法測恆星距離智慧源於生活,體現於生活。1838年,人類終於從生活的經驗中首先想到了測定星體的距離。當時所用的方法就是今天要介紹的“視差法”。
視差就在我們身旁。試看看遠處的一個物體,在鼻子前舉起一直手指,並且閉上一隻眼,用另一隻眼觀看,反覆交換兩隻眼,會發現相對於時鐘,手指好像跳了位置。這就是視差。把手伸直,你會發現跳變的位置好像小了一點。因為有視差,我們才能分辨物體的遠近,產生距離感。
用在測距方法上,兩眼之間的距離叫做“基線”,手指與兩眼所成角叫做“視差角”。如下圖所示:
恆星視差與距離
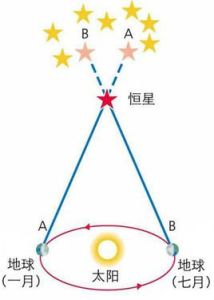
在地球上觀測恆星也有視差現象。此時基線就是地球軌道的直徑,被觀測恆星的視差就是太陽、恆星與地球所形成的內角P,隨著地球公轉,恆星就如下圖所示出現周年視差運動,恆星距離我們愈近(d),視差p就愈大,反之亦然。
由於大部分的恆星的距離實在太遠,視差都非常小。離我們最近的恆星(半人馬比鄰星)的視差只有0.75角秒,連1角秒(1/3600度)也不到。加上地面觀測,大氣影響,誤差很大。所以視差法只適用於度量300光年以內的恆星距離。
秒差距
秒差距(ParSec)是天體距離的單位,有視差(Parallax)及角秒(Arc-Seconds)連個英文合成,簡稱PC,是周年視差P的倒數1/P。天體的周年視差為1角秒時,他距離我們為1秒差距。由於1角秒所對應的兩條邊的長度差異完全可以忽略,因此,這個三角形可以想像成直角三角形,也可以想像成等腰三角形。
1秒差距=206265A.U.=3.26光年。大家可以看下圖所示:
 三角視差法測恆星距離
三角視差法測恆星距離我們來具體推導一下計算方法
1、當P很小(<=1角秒),R=R'。因此,設定P=1角秒,這是PC=1
2、滿足上麵條件之後,地日的距離1AU可以看成近似以R為半徑的圓周的一個部分。
3、按比例得出計算:
1A.U./2ΠR=1秒/360*60*60秒註:1角秒=1/3600度
R=1/(2Π)*360*60*60A.U.=206265A.U.=3.26光年
以上就是利用角秒和秒距離的概念給出了天體物理學中測量近距離恆星的一個簡單三角視差法。
視差法測距原理
如圖2.1-2,在B點觀察幾十米以外的物體D,A為BD延長線上極遠處的一個參考點。人沿垂直於ADB方向移動到C點(BC稱為基線)再觀察D。由於A點極遠,可以認為BA∥CA,即∠θ=∠θ′。在CD線上取點S過SO作SO⊥CA,可以看出ΔBCD∽ΔOSC,如果OS、OC和BC長度已知,則
BD=(OC/OS)BC
按此法測得的BD誤差較大,用下面的方法可以減少測量誤差。
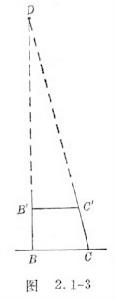
如圖2.1-3,由B點觀察被測點D,記下B點位置和BD方向。沿BD的垂直方向將觀察點由B點移到C點重新觀察D點,記下C點位置和CD方向。在BD和CD線上截取BB′=CC′。由於BD>>BC,故B、C可以看成以D為圓心,DB為半徑的圓弧上的兩點,所以只要測出BB′、B′C′、BC,即可計算出BD。
存在的誤差
現代天文學認為,太陽系外最近的一顆恆星與太陽的距離為4.2光年,然而,我們根據對用肉眼觀測到的天文現象進行分析和計算發現,這一數據存在嚴重的錯誤!
1、用肉眼觀測到的天文現象
一九八三年夏天,有一顆明亮的星從天上飛過:設觀測點的正上方為參考點,觀測角度分前30度和後30度,時間為前3天和後3天。在前30度到後30度,該星以直線飛行,然而,在後30度處,該星與在後30度處的一顆靜止的明亮的星發生了相互吸引作用,作用的結果如同二個大小和質量都相等的剛性的球發生碰撞作用,結果使二顆明亮的星朝不同的方向飛行,二顆明亮的星的飛行方向的夾角為100度左右。
該靜止的星應該是一個遙遠的天體,而不應該是太陽系內的行星。否則,這是太陽系內發生的重大天文事件而被專業的天文學家發現、觀測和記錄,並且行星也飛離了原來的軌道。
如果該靜止的星是太陽系外的星,那么,能夠被肉眼觀測到的明亮的星應該是恆星。由於二顆明亮的星的大小和亮度是一樣的,因此,我們可以認為是同太陽一樣大小和亮度的恆星。
我們設參考點前30度、參考點後30度和觀測點為正三角形,這樣,二顆星發生相互吸引作用時與觀測點的距離等於該星六天飛行的距離。如果該靜止的星與觀測點的距離為4.2光年,那么,該飛行的星的速度為4.2×365.25/6 =255,即該星的飛行速度是光速的255倍!我們認為:這是不可能的!
2、關於三角視差法的誤差原因
我們知道,測量天體之間的距離是一件不容易的事。天文學家利用三角視差法測量離我們比較近的天體的距離。三角視差法是把被測的那個天體置於一個特大三角形的頂點,地球繞太陽公轉的軌道直徑的兩端是這個三角形的另外二個頂點,通過測量地球到那個天體的視角,再用到已知的地球繞太陽公轉軌道的直徑,依靠三角公式就能推算出那個天體到我們的距離了。
然而,三角視差法是以光的直線傳播為基礎的。中學的物理上就知道,光在不同介質中傳播會發生折射,如何去掉地球大氣的影響是個問題,這點或許利用在太空的哈勃之類來代替觀察,可以消除地球大氣的影響,但是,太陽系內的影響呢,太陽系內就沒有其他介質了么?光不會發生折射嗎?另外,光線在太陽引力的作用下會發生彎曲,這樣光線就不是直線了。這裡都存在凸透鏡效應。
一顆高速飛行的恆星可以通過與另一顆靜止的恆星的相互吸引作用,使另一顆靜止的恆星產生高速飛行,這樣,在未來的天空中必將存在許多顆高速飛行的恆星,現代天文學家的觀測應該能夠證明這一點。由於二顆星的相互吸引作用發生於一九八三年,因此,如果能夠確定二顆恆星發生相互吸引作用時的位置和光度以及現在的位置和光度,對於研究其他恆星的距離和運動速度等將具有重要的意義。