三角形奠基法

三角形奠基法(construction method by frist construct some triangle)是題解作圖的一種常用方法。三角形是最簡單的多邊形，因此，只要很少的條件，就可把它作出來，在有些作圖題中，先作成所求圖形中的某個三角形，實際上便奠定了全部圖形的基礎，由此就可以逐步做出其餘部分，這樣的三角形，可稱奠基三角形。利用奠基三角形作為基礎來解作圖題，叫做三角形奠基法。這個方法在作圖中經常套用，有許多問題藉助它可獲得解決 。

基本介紹

解某些作圖題時，如果先作出圖形中的某個三角形，然後在此基礎上作出所要求作的圖形，此種解作圖題的方法稱為 三角形奠基法，該三角形稱為作圖的 奠基三角形。

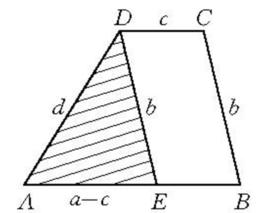
例如，已知四條線段a，b，c，d，求作梯形ABCD，使AB=a，BC=b，CD=c，DA=d，AB∥CD。該作圖題的思路要點是：假設梯形ABCD已經作出，且AB=a，BC=b，CD=c，DA=d，作DE∥BC，則DE=b，AE=a-c，於是△AED可以確定(如圖1)，並成為奠基三角形，在此基礎上，所求作的梯形極易作出，當a，b，a-c中最大者小於其他兩線段之和時該作圖題有解，否則無解 。

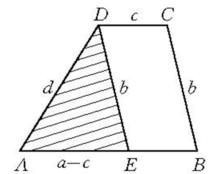圖1

例如，已知三角形的邊a，以及這邊上的高h和中線m，作此三角形。如下圖所示。假定△ABC已作出。由條件知R△AHM是確定的，以該三角形為基礎，作出BC=a，則得B、C兩點。連結AB、AC，就得到△ABC 。

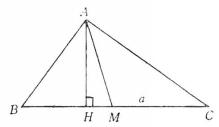圖2

例題分析

【例1】已知第一邊的長，第二邊上的高，第三邊上的中線，求作三角形。

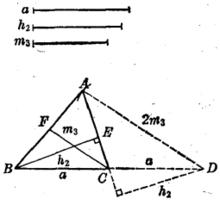圖3

已知 三線段a、h、m。

求作 △ABC，使邊BC=a，高BE=h，中線CF=m。

分析 設圖已成(圖3)，在直角三角形△BCE中，已知斜邊BC=a及一腰BE=h，故此三角形得以確
定，確定此三角形後，若延長BC至D使CD=a，並連DA，則DA=2CF=2m；因此A點可求。

作圖先作△BCE，使
∠BEC=90°，BE=h，BC=a，
其次延長BC至D，使CD=a，最後以D為圓心、2m為半徑畫弧設交直線CE於A，並連AB。這樣作得△ABC就是所求三角形。

證明 作出△ABC的中線CF，由於BC=CD，得知

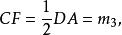三角形奠基法

又BE是△ABC的一高，且

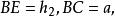三角形奠基法

故△ABC合乎所要求的條件。

推究 本題有無解答，只與a和h的大小有關係；而解答個數，則和三已知線段的長短都有關聯，其各種情形可歸納如下：

(1) a>h時，若

1° h<2m≠a，則有二解；

2° h=2m或a=2m，則有一解；

3° h>2m，則無解。

(2) a=h時，若

1° h<2m，則有一解；

2° h≥2m，則無解。

(3) a<h時，無解 。