計算方法
找尋三角平方數的問題可用以下方法簡化成佩爾方程。每個平方數的形式為m^2，三角形數的則為n(n+1)/2。於是求n, m使得：
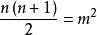三角平方數變形得到：
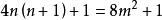三角平方數
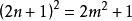三角平方數將a=2n+1，b=2m代入，得到方程
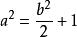三角平方數上述方程即為佩爾方程。
n與m的遞推公式為：
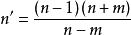三角平方數
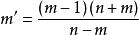三角平方數n與m的通項公式為：
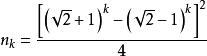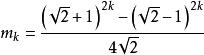三角平方數
三角平方數下面是一些三角平方數：
| 序號 | 三角平方數 | n | m | n+m | n-m | 大衛.蓋爾問題 |
| 1 | 1 | 1 | 1 | 2 | 0 | 0=0 |
| 2 | 36 | 8 | 6 | 14 | 2 | 1+……+5=7+8 |
| 3 | 1225 | 49 | 35 | 84 | 14 | 1+……+34=36+……+49 |
| 4 | 41616 | 288 | 204 | 492 | 84 | 1+……+203=205+……+288 |
| 5 | 1413721 | 1681 | 1189 | 2870 | 192 | 1+……+1188=1190+……+1681 |
前後兩個n或m的比值趨於2*sqrt（2）+3。
相關問題
大衛·蓋爾曾提出一條問題：求對於哪些 n，使得1,2,3,4..., n這個數列中，存在一個數 s，在 s之前的數之和跟在 s之後的數之和相等。例如1,2,3,...,8中，6就是這樣的一個數，1+2+3+4+5=7+8
解答： 根據題意列方程，得到 s( s-1)/2 = ( s+ n+1)( n- s)/2, s^2= n( n+1)/2
當第 n個三角形數是平方數時，就符合題目的條件。
