∑類

∑類是一類單葉函式，它是由全體在單位圓外具有展開式g(z)=z+b0+b1z+b2z(1

簡介

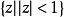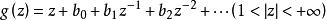∑類

∑類

∑類是一類單葉函式，它是由全體在單位圓外具有展開式的單葉函式構成的集合。

單葉函式

單葉函式是複變函數中一類重要的解析函式。對複平面區域D上單值的解析函式ƒ(z)，若對D中任意的不同的兩點z、z有ƒ(z)≠ƒ(z)，則說f(z)為D上的單葉函式。

單葉函式及其相關的單葉映射等課題是複變函數論最重要的研究內容之一。單葉函式具有很多比較好的性質，例如：單葉函式最基本的性質為其導數無零點；單葉函式的單葉函式仍為單葉函式；單葉函式的反函式仍為單葉函式。

意義

20世紀初，在對單位圓盤內滿足規範條件f(0)=f'(0)-1=0的單葉解析函式類（S類）以及單位圓外以∞為單極點且留數為1的單葉函式類（∑類）的研究中，格朗沃爾面積定理、克貝1/4定理、克貝偏差定理等顯示單葉函式研究的序幕。